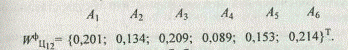Иерархический синтез приоритетов альтернатив, проведенный для второго прямого процесса, позволил получить следующий вектор приоритетов исходов:
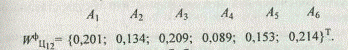
Интегральная оценка обобщенного исхода, полученная относительно фокуса иерархии второго прямого процесса, имеет следующее значение:
ОИф12= 19,616.
Анализ интегральных оценок обобщенных вероятных исходов для первого (10,476) и второго (19,616) прямых процессов указывает на уменьшение во второй итерации различия между вероятным и желаемым (21,290) исходами.
Во втором прямом процессе получен достаточно хороший результат по критерию интегральной оценки обобщенного исхода, поэтому итерационный процесс на этом этапе может быть завершен.
Контрольные вопросы и задания
Дайте определение иерархическим уровням применительно к задачам аналитического планирования. Охарактеризуйте прямой и обратный процессы аналитического планирования. На основе каких предпосылок и к...
Литература
Саати Т., Керне К. Аналитическое планирование. Организация систем: Пер. с англ. — М.: Радио и связь, 1991. — 224 с. Аганбегян А. Г. Перспективное отраслевое планирование: Экономико-математические...
Элементы теории нечетких множеств
Рассмотрим основные элементы теории нечетких множеств. Пусть U— полное множество, охватывающее все объекты некоторого класса. Нечеткое подмножество F множества U, которое в дальнейшем будем называ...
Элементы теории нечетких множеств 2
Функция принадлежности для элементов нечеткого множества F1, соответствующих понятию высокие процентные ставки (рис. 4.1), будет иметь следующий вид: Функция принадлежности к нечеткому множеству н...
Нечеткие операции, отношения и свойства отношений
Операции над нечеткими множествами. Над нечеткими множествами, как и над обычными, можно выполнять математические операции. Рассмотрим важнейшие из них: дополнение множества, объединение и пересеч...
Нечеткие отношения.
Нечетким отношением R между полным множеством U и другим полным множеством V называется подмножество прямого декартова произведения U V, определяемое следующим образом: где U = {u1, u2,..., иl}, V...
Свойства нечетких отношений.
1. Объединение отношений (R S)(u, v) = R(u, v) S(u, v), и U, v V. 2. Пересечение отношений (R S)(u, v) = R(u, v) S(u, v), и U, v V. 3. Операция включения (R S) « R(u, v) S (u, v), u U, v V. 4. Сво...
Многокритериальный выбор альтернатив на основе пересечения нечетких множеств
Элементы теории нечетких множеств успешно применяются для . принятия решений. Экспертные оценки альтернативных вариантов по критериям могут быть представлены как нечеткие множества или числа, выра...
Многокритериальный выбор альтернатив на основе пересечения нечетких множеств 2
Лучшей считается альтернатива a*, имеющая наибольшее значение функции принадлежности Если критерии Сi имеют различную важность, то их вклад в общее решение можно представить как взвешенное пересеч...
Многокритериальный выбор альтернатив на основе нечеткого отношения предпочтения
Рассмотрим метод принятия решений, предполагающий построение множества недоминируемых альтернатив на основе нечеткого отношения предпочтения. Постановка задачи в краткой форме представляется следу...
Многокритериальный выбор альтернатив 2
Определение 3. Пусть А — множество альтернатив и mR — заданное на нем нечеткое отношение предпочтения. Нечеткое подмножество недоминируемых альтернатив множества (А, mR) описывается функцией прина...
Многокритериальный выбор альтернатив 3
Строится нечеткое отношение Q2: и определяется нечеткое подмножество недоминируемых альтернатив в множестве (A,mQ2): Данная функция упорядочивает альтернативы по степени их недоминируемости. Числа...
Многокритериальный выбор альтернатив 4
Отыскивается пересечение множеств mQ1НД и mQ2НД: Рациональным считается выбор альтернатив из множества Наиболее рациональной альтернативой из множества АНД является та, которая имеет максимальную...
Многокритериальный выбор альтернатив с использованием правила нечеткого вывода
Рассмотрим метод многокритериального выбора альтернатив на основе композиционного правила агрегирования описаний альтернатив с информацией о предпочтениях лица, принимающего решение, которые задан...
Многокритериальный выбор 2
Тогда высказывание (4.1) можно записать в виде: Для придания общности суждениям обозначим базовые множества U и V через W. Тогда Аi — нечеткое подмножество W, в то время как Вi — нечеткое подмноже...
Многокритериальный выбор 3
Удовлетворительность альтернативы, которая описывается нечетким подмножеством А из W, определяется на основе композиционного правила вывода: G = А ° D, где G — нечеткое подмножество интервала I. Т...
Многокритериальный выбор 4
при 0 a1 b1 а2 b2 ... аn bn 1. Тогда точечное значение для множества С можно записать в виде: где amax — максимальное значение в множестве С. При выборе альтернатив для каждой из них находится удо...
Многокритериальный выбор альтернатив на основе аддитивной свертки
В рассматриваемом методе экспертные предпочтения представлены с помощью нечетких чисел, имеющих функции принадлежности треугольного вида (рис.4.2). Пусть имеется множество альтернатив А = {а1, а2,...
Многокритериальный выбор альтернатив на основе аддитивной свертки 2
Если функции принадлежности mRij(rij) и mai(ai) имеют треугольный вид, то для них, как и для нечеткого числа X, вершина X*, а также левая Х и правая X границы определяются следующими соотношениями...
Ранжирование альтернатив на множестве лингвистических векторных оценок
Задано множество альтернатив A == {а1, а2, ..., аm} и множество соответствующих исходов S = [s1, s2, ..., sm,}. Каждый исход sj характеризуется альтернативой аi и вектором лингвистических оценок н...
Ранжирование альтернатив 2
Степень истинности m (sj, sk) нечеткого высказывания sj sk можно определить как вероятность того, что точное значение sj будет меньше точного значения sk. Предполагая, что исходы являются независи...
Ранжирование альтернатив 3
Так как между множеством альтернатив и исходив существует взаимно однозначное соответствие, функцию принадлежности нечеткого отношения предпочтения на множестве альтернатив можно представить в вид...
Банковское кредитование
С развитием рыночных отношений процесс кредитования банками предприятий сопряжен с многочисленными факторами риска, способными повлечь за собой непогашение ссуды в установленный срок. При анализе...
Банковское кредитование 2
Таблица 4.1 Данные бухгалтерской отчетности Финансовый показатель Значение показателя...
Банковское кредитование 3
Перечисленные коэффициенты являются критериями качества кредитоспособности предприятий и рассчитываются по следующим формулам: Рассчитанные значения критериев качества для рассматриваемых предприя...
Банковское кредитование 4
Этап 1. Построение функций принадлежности, соответствующих понятиям предпочтительный коэффициент абсолютной ликвидности, желаемый промежуточный коэффициент покрытия, наилучший коэффициент рентабел...
Банковское кредитование 5
Этап 3. Производится свертка имеющейся информации в целях выявления лучшей альтернативы. Множество оптимальных альтернатив В определяется путем пересечения нечетких множеств, содержащих оценки аль...
Банковское кредитование 6
Если критерии, по которым осуществляется выбор вариантов, имеют одинаковую важность для ЛПР, то правило выбора лучшего варианта имеет вид: В = F1 F2 F3 F4 F5. Оптимальной считается альтернатива с...
Выбор лучшего банка для размещения денежных средств физическим лицом
Цель решаемой задачи — выбор лучшего банка для размещения денежных средств физическим лицом. В отличие от предыдущего примера используемые для выбора критерии имеют различную значимость для ЛПР. Б...
Выбор лучшего банка 2
Таблица 4.3 Значения критериев для альтернатив Критерий Альтернатива...
Выбор лучшего банка 3
На рис. 4.4 приведена экранная форма системы принятия решений на нечетких множествах, которая используется для ввода исходной информации о критериях и альтернативах. Критерии имеют различную значи...
Выбор лучшего банка 4
Для критериев, использованных при решении задачи выбора лучшего банка, составлена следующая матрица: Выбор банка F1...
Выбор лучшего банка 5
Таблица 4.4 Собственный вектор матрицы полярных сравнений критериев и их весовые коэффициенты Множество оптимальных альтернатив В с учетом различной важности критериев качества определяется путем...
Выбор конкурентоспособного товара методом нечеткого отношения предпочтения
Под конкурентоспособностью понимают комплекс потребительских, стоимостных и социальных характеристик товара (изделия), определяющих его успех на данном рынке, т. е. способность данного товара быть...
Выбор конкурентоспособного товара 2
На основании функций принадлежности всех альтернатив по восьми критериям определены их конкретные значения, которые представляют собой следующие нечеткие множества: По этим данным составлены матри...
Выбор конкурентоспособного товара 3
Задача выбора решается в соответствии с описанной выше процедурой. Строим нечеткое отношение Q1 = R1 R2 … R8:...
Выбор конкурентоспособного товара 4
Находим подмножество недоминируемых альтернатив на множестве {А, }: по всем i и j (i j):...
Выбор конкурентоспособного товара 5
2. Строим отношение Q2. Коэффициенты wk относительной важности критериев имеют следующие значения: w1 = 0,23, w2 = 0,09, w3 = 0,04, w4 = 0 23 w5 = 0,04, w6 = 0,09, w7 = 0,23, w8 = 0,04....
Выбор конкурентоспособного товара 6
Определяем нечеткое отношение Q2. Находим подмножество недоминируемых альтернатив множества [А, }: по всем i и j (i j): 3. Результирующее множество недоминируемых альтернатив есть пересечение множ...
Метод нечеткого логического вывода в задаче выбора фирмой кандидата на замещение вакантной должности бухгалтера
Руководство фирмы рассматривает кандидатов на замещение вакантной должности бухгалтера. Задача заключается в том, чтобы, используя описанный выше метод, выявить наилучшего претендента. Обсуждение...
Метод нечеткого логического вывода 2
Для формулирования правил следует определить возможные значения лингвистических переменных Xi и Y, которые будут использоваться для оценки кандидатов: d1: Если Х1 = ПОДХОДЯЩЯЯ и X2 = ВЫСШЕЕ, и Х3...
Метод нечеткого логического вывода 3
В рассматриваемой задаче оценки кандидатов заданы следующими нечеткими множествами: ПОДХОДЯЩАЯ (квалификация) А = {0,8/u1, 0,61u2, 0,5/u3, 0,1/u4, 0,3/u5}; ВЫСШЕЕ (образование) В = {0,5/u1,1/u2, 0...
Метод нечеткого логического вывода 4
Теперь правила можно записать в виде: Используя для преобразования правил вида Если Х = М, то Y = Q импликацию Лукасевича mD(u, j) = min(l, 1-mM /(u) + mY (j)), для каждой пары (u, j) U х J получа...
Метод нечеткого логического вывода 5
Метод нечеткого логического вывода 6
В результате пересечения отношений D1, ..., D6 получаем общее функциональное решение: Для вычисления удовлетворительности каждой из альтернатив применим правило композиционного вывода в нечеткой с...
Метод нечеткого логического вывода 7
Отсюда (i) = (uk, i) Другими словами, Еk есть k-я строка в матрице D. Теперь применим описанную выше процедуру для сравнения нечетких подмножеств в единичном интервале для получения наилучшего реш...
Метод нечеткого логического вывода 8
Аналогично находим точечные оценки для других альтернатив: для второй альтернативы F(E2) = 0,656; для третьей — F(E3) = 0,575; для четвертой — F(E4) = 0,483; для пятой — F(E5) = 0,562. В качестве...
Метод нечеткого логического вывода 9
Тогда соответствующие левым частям правил нечеткие множества Мi, i = 1, .... 6, i 4, будут иметь вид: F(u1)—0,560; F(u2)— 0,600; F(u3)—0,575; F(u4)— 0,475; F(u5)— 0,530....
Метод нечеткого логического вывода 10
Сравнение полученных результатов показывает, что с повышением значимости критерия Х4 ранжировка альтернатив несколько изменилась: и1 и u5 поменялись местами. Этот факт согласуется с исходными данн...
Метод нечеткого логического вывода 11
При мягком подходе к принятию решения получены следующие точечные оценки альтернатив: F(u1) - 0,494; F(u2) - 0,533; Р(u3) - 0,530; Р(u4) - 0,437; Р(u5) - 0,539. Полученные результаты можно интерпр...
Метод нечеткого логического вывода 12
Рассмотрим решение задачи о выборе бухгалтера с использованием такой системы. Для этого введем следующие лингвистические переменные: ОБРАЗОВАНИЕ (Высшее, Среднее) ОПЫТ (Отсутствует, Приемлемый, Бо...
Метод нечеткого логического вывода 13
Значения лингвистических переменных для альтернатив u1, ..., u5 приведены в табл. 4.6. Таблица 4.6 Исходные данные для логического вывода Лингвистическая переменная...
Метод нечеткого логического вывода 14
На рис. 4.6 и 4.7 показаны экранные формы интеллектуальной программной системы нечеткого логического вывода, используемые для ввода исходной информации....
Метод нечеткого логического вывода 15
В табл. 4.7. приведены результирующие лингвистические оценки альтернатив, полученные методом нечеткого вывода, и соответствующие им значения мер сходства....
Метод нечеткого логического вывода 16
Таблица 4.7 Результаты работы системы нечеткого вывода Лингвистическая оценка Альтернатива...
Выбор фирмой стратегии расширения доли рынка методом аддитивной свертки
Рассмотрим пример применения метода аддитивной свертки для решения задачи по выбору некоторой фирмой, производящей бытовую технику, стратегии расширения своей доли на рынке. Первоначально определя...
Выбор фирмой стратегии расширения 2
Для оценки альтернатив определим следующие критерии: c1 — затраты на расширение производства; c2 — время реализации проекта; c3 — затраты на маркетинговые исследования; с4 — управленческие расходы...
Выбор фирмой стратегии расширения 3
Критерии получили следующие лингвистические оценки относительной важности a = { = ВАЖНЫЙ; = ДОВОЛЬНО ВАЖНЫЙ; = НЕ ОЧЕНЬ ВАЖНЫЙ; = ВАЖНЫЙ; = НЕ ОЧЕНЬ ВАЖНЫЙ; = ДОВОЛЬНО ВАЖНЫЙ; = ВАЖНЫЙ; = НЕ ОЧЕНЬ...
Выбор фирмой стратегии расширения 4
Таблица 4.8 Оценка удовлетворительности альтернатив относительно критериев Критерий Оценка альтернативы...
Выбор предприятия для кредитования методом лингвистических векторных оценок
Решается задача выбора из трех альтернативных предприятий наиболее платежеспособного в целях предоставления кредита. Оценка альтернатив (аi) проводится по следующим критериям: с1 — общая ликвиднос...
Выбор предприятия для кредитования 2
Лингвистические векторные оценки альтернатив заданы матрицей: Суть данной методики заключается в вычислении оценки предпочтительности каждой из альтернатив относительно других. При этом, как и в с...
Выбор предприятия для кредитования 3
Аналогично находятся суммы по критериям c2 и c3. Функция принадлежности m(a1) вычисляется следующим образом:...
Выбор предприятия для кредитования 4
Теперь вычислим нечеткое отношение m(a1): Степень предпочтительности альтернативы а1 равна минимальному из приведенных значений, т. е, m(a1) = 0,673. Для альтернативы а2 получены следующие оценки:...
Сравнительный анализ различных методов принятия решений
Теория нечетких множеств, предложенная Л. Заде в 1961 г., к настоящему времени приобрела широкую популярность и получила практическое применение во многих отраслях знаний. В сфере принятия решений...
Характеристика критериев
Рентабельность инвестиций (PI) — это показатель, позволяющий определить, в какой мере возрастает ценность фирмы (богатство инвестора) в расчете на один рубль инвестиций. Рентабельность показывает...
Описание альтернатив
1. Проект по созданию технологии и оборудования для термического обезвреживания и переработки отходов (a1). В данном проекте предлагается метод переработки отходов, основанный на их последовательн...
Решение задачи методом максиминной свертки
Оценки альтернатив по заданным критериям представлены следующими нечеткими множествами: Весовые коэффициенты важности рассматриваемых критериев определены с использованием процедуры парного сравне...
Решение задачи с использованием метода отношений предпочтения
На основании функций принадлежности (4.3) построены следующие отношения предпочтения на множестве альтернатив: Множество недоминируемых альтернатив = ||1 1 1||. Значение нормированных на единицу в...
Решение задачи с использованием метода отношений предпочтения 2
Вычислим нечеткое отношение Q2: Находим подмножество недоминируемых альтернатив множества {А, }: (аi) = || 0,83 0,69 1 ||. Результирующее множество недоминируемых альтернатив — это пересечение мно...
Решение задачи с применением нечеткого логического вывода
На основании приведенных выше исходных данных о критериях и альтернативах экспертом сформулированы правила: d1 : Если с1 = ВЫСОКАЯ, и с2 = ХОРОШАЯ, и с3 = ПРИЕМЛЕМЫЕ, то Y = УДОВЛЕТВОРИТЕЛЬНЫЙ; d2...
Решение задачи с применением нечеткого логического вывода 2
ПРИЕМЛЕМЫЕ (первичные средства) G = {0,3/a1, 0,5/a2,1/a3}; НИЗКИЙ (производственный риск) D = {0,5/a1, 0,3/а2, 0,9/a3}; НИЗКИЙ (инвестиционный риск) Е = {0,6/a1, 0,4/а2, 0,2/a3} ОЧЕНЬ НИЗКИЙ (инве...
Решение задачи с применением нечеткого логического вывода 3
Правила приобретут следующий вид: Используя для преобразования правил импликацию Лукасевича, получим нечеткие отношения D1, ... D3 на U x J и в результате их пересечения функциональное решение D:...
Решение задачи методом аддитивной свертки
Важность критериев была задана нечеткими числами с функциями принадлежности следующего вида: ВАЖНЫЙ (В)— mB ={0,4; 1/0,7; 0/1}; ОЧЕНЬ ВАЖНЫЙ (OB) — mOB ={0/0,7; 1/1}; НЕ ОЧЕНЬ ВАЖНЫЙ (НОВ) — mHOB...
Решение задачи методом аддитивной свертки 2
Взвешенные оценки альтернатив Ri имеют следующие функции принадлежности: Оценки предпочтительности альтернатив равны: m(a1) = 0,90, m(a2) = 0,62, m(a3) = 1,0. Лучшей альтернативой является a3, a х...
Решение задачи методом анализа иерархий
На заданном наборе критериев была построена трехуровневая иерархия, на верхнем уровне которой определена цель выбора (сG). На втором уровне находятся обобщенные критерии: прибыль (сP) к и риск (сR...
Сравнение полученных результатов
На рис. 4.9 приведены результаты решения задачи выбора рационального инвестиционного проекта, полученные различными методами. Несмотря на то, что исходная информация во всех рассмотренных примерах...
Сравнение полученных результатов 2
Несовпадение результатов, полученных разными методами, объясняется, с одной стороны, разными способами представления экспертной информации, а с другой стороны — различием подходов к принятию решен...
Контрольные вопросы и задания
Перечислите и дайте определения основным элементам теории нечетких множеств. Дайте определение нечетким операциям, отношениям и свойствам отношений. Охарактеризуйте постановку задачи многокритериа...
Литература
Заде Л. Понятие лингвистической переменной и его применение к принятию приближенных решений: Пер. с англ. — М.: Мир, 1976. — 165 с. Нечеткие множества и теория возможностей. Последние достижения:...
МЕТОДЫ КОМБИНАТОРНО-МОРФОЛОГИЧЕСКОГО АНАЛИЗА И СИНТЕЗА РАЦИОНАЛЬНЫХ СИСТЕМ
Методы комбинаторно-морфологического анализа и синтеза предназначены для поиска новых решений на основе разделения рассматриваемой системы на подсистемы и элементы, формирования подмножеств альтер...
Классификация задач анализа и синтеза систем
Задачи морфологического синтеза отличаются большим разнообразием и классифицируются по различным признакам, характеризующим количество и качество доступной информации. В общем случае задачи морфол...
Классификация задач анализа и синтеза систем 2
F — отображение множества допустимых альтернатив, реализующих функции, в множество критериальных оценок отображение А в К может иметь детерминированный вид (f1); вероятностный (f2); неопределенный...
Классификация задач анализа и синтеза систем 3
Р — число рассматриваемых уровней системы p1 — один; p2 — более одного; Y — уровень формализации постановки и решения задачи у1 — неформализованный эвристический подход; у2 — формально-эвристическ...
Постановка задач анализа и синтеза систем
Целями морфологического анализа и синтеза систем являются: системное исследование всех мыслимых вариантов решения задачи, вытекающих из закономерностей строения (морфологии) совершенствуемого объе...
Постановка задач анализа и синтеза систем 2
В приведенном выражении приняты следующие обозначения: Kl — число способов (альтернатив) для реализации l-и функции или обобщенной подсистемы; L — число всех функций. Морфологическое множество явл...
Постановка задач анализа и синтеза систем 3
Этап 2. Осуществляется построение морфологической таблицы и заполнение ее альтернативами. Этап 3. Описываются свойства альтернатив морфологической таблицы. Свойства альтернатив могут характеризова...
Установление исходной цели синтеза
Формирование исходной цели синтеза может осуществляться с различной степенью полноты и определенности. Если перед исследователем поставлена задача, требующая поиска принципиально новой социально-э...
Способы формирования поисковых заданий
Можно выделить три подхода к формированию формализованных поисковых заданий, на основании которых решаются различные задачи морфологического синтеза. В соответствии с первым подходом поисковое зад...
Процедура 1.
В соответствии с этой процедурой поисковое задание формируется непосредственно на морфологической таблице в виде комбинаций альтернатив {Aij}, извлекаемых по одной из каждой строки таблицы. Оценка...
Процедура 2.
Поисковое задание формируется в виде некоторого гипотетического идеального варианта, элементы которого Aij, соответствующие каждой строке морфологической таблицы, имеют по всем заданным критериям...
Процедура 3.
Поисковое задание может формироваться на основании желаемого для эксперта качества, которое необходимо иметь в синтезируемых вариантах систем. При формировании поискового задания методом сравнения...
Морфологические таблицы
Морфологические таблицы — эффективное средство представления знаний о множестве социально-экономических или организационных систем. Они позволяют систематизировать достаточно большой объем знаний...
Разработка морфологических таблиц на основе функционально-элементного анализа систем
При разработке морфологических таблиц, предназначенных для синтеза рациональных и оптимальных вариантов по многим критериям качества, классификационные признаки и их значения должны иметь такое со...
Разработка морфологических таблиц 2
На основании проведенного анализа формируются строки морфологической таблицы, в которые записываются функции системы или обобщенные функциональные подсистемы, из которых состоит система в целом. П...
Разработка морфологических таблиц с использованием классификационных признаков
При разработке морфологических таблиц на основе функционального анализа систем достаточно было выявить функции подсистем, образующих исследуемую систему в целом, и подобрать для каждой функции аль...
Разработка морфологических таблиц с использованием классификационных признаков 2
Основы кластерного анализа систем
Для выявления закономерностей строения сложных систем целесообразно в первую очередь собранные данные разложить по полочкам, классифицировать. Вопросы кластерного анализа рассмотрены в учебнике А....
Системы-классификации
Система определяется как непустое множество объектов (или несколько таких множеств), между которыми установлены некоторые отношения. Таким образом, в системе набор элементов рассматривается как це...
Система-модель
С = С ( I, R, A(S), A(ps) , A(SP) ) является образом системы-оригинала С' = С ( I', R', А(S')), A(RS'), A(SR')). Отображение множества С' на множество С является гомоморфным, если С имеет тот же с...
Основные этапы построения и исследования систем-классификаций
Первым этапом классификационных построений является глубокое проникновение в суть рассматриваемых явлений и выбор соответствующего принципа классификации. Второй этап — установление списка признак...
Виды измерений
Системы, подлежащие классификации, изучаются прежде всего относительно наличия у них характерных свойств или состояний, которые отражаются различными признаками. Значения признаков могут измерятьс...
Формализация обработки качественных признаков
Множество вариантов, систематизированных в морфологических таблицах, может быть отражено списком качественных признаков. Список признаков, определяющий вариант морфологического множества, представ...
Формализация обработки качественных признаков 2
Формула (5.1) читается: семейство множеств S, состоящее из всех Sj, таких, у которых элементы j принадлежат множеству J. Аналогично семейство множеств есть индексированное множество, а I — индексн...
Меры сходства и различия.
Мерой сходства (близости) обычно называется величина С (Sj, Sk), имеющая предел и возрастающая с возрастанием близости объектов. Под мерой сходства будем понимать неотрицательную вещественную функ...
Меры сходства и различия 2
Меры сходства и различия изобретаются по специальным правилам [4], а выбор конкретных мер зависит, в первую очередь, от суперзадачи — цели конкретного исследования, а также от шкалы измерений. В т...
Меры сходства и различия 3
Вычисление значений меры сходства двух сравниваемых объектов по качественным признакам удобно производить на основе бинарной матрицы, которая в терминах теории множеств задается следующим образом:...
Меры сходства и различия 4
Вычисление меры сходства, например, по формуле Чекановского — Серенсена (см. табл. 5.4) с учетом бинарной матрицы (5.4) осуществляется по следующему выражению: где xi1, xi2 — одно из двух значений...
Мера включения.
Она отражает различную степень включения одного объекта в другой и позволяет выявить, какой из двух сравниваемых объектов содержит больше специфических признаков, т. е. определить, какой объект бо...
Отношения мер сходства, включения и иерархии
Отношения мер сходства (различия), включения и иерархии позволяют при обработке множеств исследуемых объектов выявлять наиболее интересные закономерности строения анализируемых множеств. В общем с...
Отношения мер сходства, включения и иерархии 2
Например, если рассчитанные для пары объектов меры включения имеют следующие значения: W(S1; S2) = 0,57, W(S2; S1)= 0,67, то эти результаты можно интерпретировать следующим образом. Мера включения...
Отношения мер сходства, включения и иерархии 3
Таким образом, на первом шаге каждый объект из заданного множества считается классом. Далее два наиболее схожих объекта объединяются в один класс, и общее число последних становится равным q -1. Э...
Алгоритм построения матриц отношений сходства и включения.
Этот алгоритм отличается для указанных двух мер лишь методом расчета значений матриц сходства и включения. Шаг 1. Формируются два множества: множество исследуемых объектов J = { S1, S2,..., Sq} и...
Шаг 2.
Генерируются все парные сочетания объектов, и для каждой пары описаний объектов Si и Sj строится индексная матрица В = xij ; i = ; j = ; где р — число строк матрицы образов, соответствующее числу...
Шаг 3.
На основе рассчитанных на шаге 2 значений мер сходства и включения (см. табл. 5.5) строятся соответствующие матрицы размерностью q x q (табл. 5.6, 5.7). Матрица мер сходства симметрична относитель...
Шаг 4.
Задается отношение сходства или включения в следующем виде: где — произвольное число (0 1,0); i, j J. Для заданного значения строится матрица сходства [С] или включения [B], в которой все значения...
Шаг 4 (2)
Матрицы [С0,60] и [B0,67] отображены соответственно графами и орграфами отношений сходства и включений (рис 5.3). Дуги и стрелки соединяют те объекты, которые имеют единицу на пересечении соответс...
Алгоритм построения иерархической классификация (дендрограммы)
Приводимый здесь алгоритм построения иерархической классификации основан на анализе значений матрицы сходства. Аналогично проводится построение иерархической классификации на основе меры различия....
Шаг 1.
Определяются два множества: множество исследуемых объектов J= {S1, S2, ..., Sq} и множество признаков Z = {Z1, Z2, ..., Zp}. Экспертно формируются индексированные множества по каждому объекту. Стр...
Шаг 2.
Просматриваются все элементы матрицы сходства [С], расположенные выше главной диагонали. Определяется и метится элемент, имеющий максимальное значение меры сходства С (Si, Sj)max (данный элемент н...
Шаг 3.
Определяются номера i-й строки j-го столбца, на пересечении которых расположен отмеченный на шаге 2 элемент. Из матрицы сходства извлекаются все значения, соответствующие i-й строке и j-му столбцу...
Шаг 4.
Определяется мера сходства классов G (Н, Н^) одним из методов, описываемых обобщенной формулой (5.6). Используем метод медианы. Тогда С учетом метода медианы имеем Hi=Si...
Шаг 5.
Процедура обработки матрицы сходства вновь начинается с шага 2. Итерационный процесс продолжается до тех пор, пока размерность матрицы сходства не уменьшится до 2 х 2. На этом процесс построения и...
Мера сходства на основе экспертной оценки
Для повышения точности определения сходства исследуемых объектов меру сходства можно формировать на основе экспертной оценки. Экспертная оценка сходства объектов проводится двумя способами. Способ...
Мера сходства на основе экспертной оценки 2
Далее составляются матрицы сходства объектов по каждому признаку и на их основе рассчитывается интегральная матрица сходства. Значения мер сходства объектов интегральной матрицы определяются по вы...
Обработка количественных признаковых образов
В работе [6] введено понятие дескриптивных множеств и определены меры пересечения и объединения двух множеств {S1 и S2) для случая применения количественных данных: где п — число признаков, предст...
Обработка количественных признаковых образов 2
Требуется найти меры сходства и включения описаний S1 и S2. Из приведенных примеров видно, что при определении числа пересечений двух множеств подсчитывается сумма минимальных значений, образующих...
Определение оригинальных и типовых систем
На основе матриц сходства и включения можно установить наиболее типовые системы или, напротив, наиболее оригинальные. Выявление указанных закономерностей осуществляется методом определения правого...
Кластеризация морфологических множеств
Генерируемые на морфологических таблицах морфологические множества вариантов систем имеют сложную неоднородную внутреннюю структуру. Выявление закономерностей строения исследуемых множеств позволя...
Кластеризация морфологических множеств 2
При втором способе описания альтернатив на основе экспертной оценки их степени сходства друг с другом расчет меры сходства между двумя вариантами S и S системы определяется по формулам: где Сl (Al...
Кластеризация морфологических множеств 3
Исходное морфологическое множество (табл. 5.12) сформировано алгоритмом лексикографического упорядочения альтернатив....
Кластеризация морфологических множеств 4
Объекты морфологического множества состоят из трех функциональных подсистем. С учетом выражения (5.8) и относящихся к нему правил формируется матрица мер сходства вариантов:...
Кластеризация морфологических множеств 5
Обработка матрицы сходства шестью указанными методами позволяет получить шесть иерархических классификаций (дендрограмм). Анализ дендрограмм (рис. 5.5) показывает, что все методы, кроме метода мак...
Кластеризация морфологических множеств 6
Классы, образованные объектами S5—S7 и S1—S3, а также S2—S4 и S6—S8, сходны между собой в среднем одной альтернативой, т. е. G(S5-7, S1-3) = G(S2-4, S6-8) = 0,5. На вид дендрограммы влияет не толь...
Кластеризация морфологических множеств 7
Проанализируем рассматриваемое морфологическое множество на предмет наличия в нем наиболее типичных и оригинальных вариантов. Для этого рассчитаем правый собственный вектор матрицы сходства: В пол...
Кластеризация морфологических множеств 8
Иерархическая классификационная структура морфологических множеств определяется прежде всего строением морфологической таблицы. В качестве примера на рис. 5.8 приведены дендрограммы, построенные м...
Многокритериальный синтез
Морфологический синтез рациональных вариантов по критериям качества начинается с независимой оценки альтернатив, принадлежащих соответствующим функциональным подсистемам. Метод основан на двух пре...
Многокритериальный синтез 2
В первом и втором способах оценки имеется возможность использовать три вида структур критериев качества, по которым предполагается ранжировать альтернативы и отыскивать рациональные элементы в каж...
Аддитивная целевая функция.
Найти подмножество S W, для элементов которого где S — подмножество искомых целостных вариантов систем; W — морфологические множества всех систем, содержащихся в исследуемой морфологической таблиц...
Мультипликативная целевая функция.
Найти подмножество S W, для элементов которого Вопрос о том, какая из этих двух средневзвешенных более адекватно отражает поведение человека, принимающего решение с учетом не одного, а нескольких...
Мультипликативная целевая функция 2
Первое значение индекс L имеет в том случае, если x1lm и x2l представляют интегральную оценку по множеству критериев качества, характеризующих альтернативу Аlm, являющуюся компонентом описания рас...
Мультипликативная целевая функция 3
Рассмотрим примеры синтеза вариантов систем на основе аддитивной целевой функции и на принципе определения меры сходства между вариантом и поисковым заданием. Используем для этой цели ранее постро...
Учет при синтезе различного вклада функциональных подсистем в эффективность целостной системы
Функциональные подсистемы, из которых состоит некоторая функциональная система, могут вносить различный вклад в ее эффективность и новизну. Поэтому в таких случаях, помимо оценки относительного вк...
Учет при синтезе различного вклада 2
Значения векторов приоритетов приписываются соответствующим элементам иерархии (см. рис. 5.10), отражающей множество функциональных реализаций. При этом рассчитанные векторы нормированы следующим...
Учет при синтезе различного вклада 3
Для упрощения примера оценка обобщенных функциональных подсистем и альтернатив производится по одному критерию, характеризующему их эффективность. При попарном сравнении обобщенных функциональных...
Учет при синтезе различного вклада 4
Анализ результатов (см. табл. 5.14) позволяет сделать следующие выводы. В тех случаях, когда равнопредпочтительны одновременно подсистемы и альтернативы (вариант 1) или только альтернативы (вариан...
Учет при синтезе различного вклада 5
Указанным вариантам соответствуют следующие комбинации альтернатив: (А11А21А32), (А11А22А31), (А11А23A31), (A12A21A31), (А13A21А31), (А11А21А31). При установлении различного вклада со стороны обоб...
Синтез систем на основе качественных классификационных признаков
Синтез вариантов систем на морфологических таблицах можно осуществлять с использованием качественных классификационных признаков, характеризующих свойства альтернатив. Классификационные признаки н...
Синтез вариантов, сходных с прототипом
Задачу поиска в морфологическом множестве вариантов систем, наиболее близких к прототипу или поисковому заданию, можно решать на основе мер сходства и различия. Целевая функция в этой задаче имеет...
Синтез вариантов, сходных с прототипом 2
Поисковые образы сгенерированных вариантов сравниваются с образом прототипа (табл. 5.17). Для каждой пары, состоящей из прототипа и поискового образа варианта, вычисляется мера сходства: C(Sll, S2...