Определяется мера сходства классов G (Н, Н^) одним из методов, описываемых обобщенной формулой (5.6). Используем метод медианы. Тогда
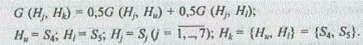
С учетом метода медианы имеем
|
Hi=Si
|
S1
|
S2
|
S3
|
S4, S5
|
S6
|
S7
|
|
С(S4,5, Si)
|
0,50
|
0,55
|
0,37
|
1
|
0,43
|
0,61
|
Полученный массив данных вписывается на место четвертой и пятой строк и четвертого и пятого столбцов вновь формируемой матрицы сходства. Наша исходная матрица сходства примет следующий вид:
|
|
S1 |
S2 |
S3 |
S4,5 |
S6 |
S7 |
|
S1 |
1 |
0,62 |
0,50 |
0,55 |
0,55 |
0,5 |
|
S2 |
0,62 |
1 |
0,46 |
0,55 |
0,50 |
0,62 |
|
S3 |
0,50 |
0,46 |
1 |
0,37 |
0,73 |
0,33 |
|
S4,5 |
0,50 |
0,55 |
0,37 |
1 |
0,43 |
0,61 |
|
S6 |
0,55 |
0,50 |
0,73 |
0,43 |
1 |
0,36 |
|
S7 |
0,50 |
0,62 |
0,33 |
0,61 |
0,36 |
1 |
На данном шаге запоминаются значения индексов вновь образованного класса (S4,5) и меры сходства, при которой этот класс образовался, — С (S4, S5) = 0,75.
