Математическая модель рефлексивного фондового рынка. Оправдавшие себя на практике модели основаны на разложении цены финансового инструмента или ее изменения в сумму двух членов – детерминированного и случайного. Впервые этот подход предложил Л. Башилье, представивший цену акции 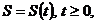
![]() где
где 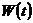
![]() - изменчивость,
- изменчивость, 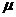
![]() Следующей удачной моделью была модель портфеля инвестиций Г. Марковица, разделившего риски инвестиций на устранимые (или диверсифицируемые) и неустранимые, зависящие от взаимного влияния финансовых инструментов на рынке. Модель Марковича для реальных торговых площадок приводила к очень большему объему вычислений, поэтому была предложена более грубая, но менее громоздкая индексная модель В. Шарга. Наконец, в связи с необходимостью страховать или хеджировать риски инвестиций была предложена модель Блэка – Шоуласа, позволявшая вычислять цену опциона С, если известны текущая цена акции
Следующей удачной моделью была модель портфеля инвестиций Г. Марковица, разделившего риски инвестиций на устранимые (или диверсифицируемые) и неустранимые, зависящие от взаимного влияния финансовых инструментов на рынке. Модель Марковича для реальных торговых площадок приводила к очень большему объему вычислений, поэтому была предложена более грубая, но менее громоздкая индексная модель В. Шарга. Наконец, в связи с необходимостью страховать или хеджировать риски инвестиций была предложена модель Блэка – Шоуласа, позволявшая вычислять цену опциона С, если известны текущая цена акции 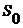
![]() , безрисковый процент
, безрисковый процент 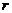
![]() и изменчивость
и изменчивость 
Все перечисленные модели, получившие название моделей случайного блуждания, были подвергнуты критике Дж. Соросом, предложившим другой подход, названный им рефлексивным. Сорос применяет этот подход к предметным областям, связанным с деятельностью человека, далеко выходящими за рамки финансовых рынков. По Соросу цены на финансовые инструменты меняются потому, что участники рынка неверно оценивают изменения этих цен в будущем, опираясь на знание этого изменения в прошлом. Поэтому действия самих участников формируют цены на рынке и, если бы участники могли не прогнозировать с какими-то вероятностями, а достоверно предсказывать будущие цены, то рынок бы застыл и цены перестали меняться. Сорос называет рефлексивным рынок. который формируют неверные действия участников. Были предприняты попытки довести эту идею Сороса до математической модели, однако, при этом не учитывалась самая важная сторона идеи Сороса. А именно, если в моделях случайного блуждания вероятности, которые влияют на цены финансовых инструментов, берутся, как нечто внешнее, т.е. или задаются априори или определяются по результатам прошлых торгов, то на рефлексивном рынке эти вероятности должны определяться в зависимости от того какой стратегии придерживается тот или иной участник рынка. Поэтому задача о построении математической модели фондового рынка может считаться решенной, если эта модель позволяет вычислить вероятности изменения цен финансовых инструментов.
Моделирования биржевой торговли 2