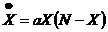Т.о. переход от классической к квантовой механике связан с переходом из одной клетки таблицы ди Бартини-Кузнецова к другой. Интерпретация результатов измерения над квантовой системой в терминах теории, построенной на другом инварианте, приводит в вероятностной интерпретации. Именно это совмещение двух разных инвариантов из таблицы ди Бартини-Кузнецова и делает квантовые системы целостными, когда ни одна из частиц, входящих в систему не является независимой от других.
Участник фондового рынка пытается определить будущие цены финансовых инструментов, опираясь на знание самих этих цен, т.е. пытается делать то же самое, что физик, который, исследуя квантовую систему, подчиняющуюся интегрируемому закону сохранения мощности, т.е. изменения энергии, пытается интерпретировать результаты исследования в терминах самой энергии. В результате и тот и другой получают только то, что и можно получить при совмещении инвариантов из разных клеток, т.е. вероятности. Но вычисление вероятностей и составляет главную задачу при построении математических моделей фондового рынка. Поэтому методология построения таких моделей заключается в получении интегрируемых законов сохранения и квантовании этих законов, т.е. переходу к неинтегрируемым законам. Поскольку правила такого перехода хорошо разработаны в квантовой теории, то появляется возможность использовать уже существующий математический аппарат для построения таких моделей. В настоящее время ведутся интенсивные работы по созданию квантового компьютера, возможности которого, если его удастся создать, по распараллеливанию вычислений фантастичны по сравнению с теми, которыми обладает классический компьютер. Одной из задач, которую можно решать на квантовом компьютере, является задача моделирования квантовых систем. Представляя рефлексивный фондовый рынок, как квантовую систему, можно избежать проблем, связанных с большим объемом вычислений, с которыми сталкиваются некоторые модели фондового рынка, основанные на теории случайного блуждания, например, модель Марковица.
Модель поведения человека И. Пригожина. Рассматривается простую модель поведения человека, имеющего выбор между несколькими возможностями, предложенную Г. Николисом и И. Пригожиным. Участник фондового рынка тоже делает выбор между разными финансовыми инструментами, в которые он может вложить деньги. Пусть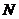 
- число людей, выбравших первую возможность, а 
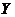
- вероятности первого и второго выбора. Тогда: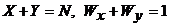 
где постоянная 
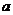
. В общем случае 
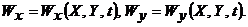
. Получается логистическое уравнение:
