П1.2.
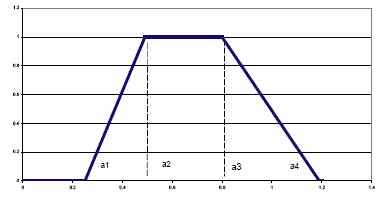
Рис. П1.2. Функция принадлежности трапециевидного числа Поскольку границы интервала заданы нечетко, то разумно ввести абсциссы вершин трапеции следующим образом:
а = (а1+а2)/2, в = (в1+в2)/2, (П1.5)
при этом отстояние вершин а1, а2 и в1, в2 соответственно друг от друга обуславливается тем, что какую семантику мы вкладываем в понатие «примерно»:
чем больше разброс квазистатистики, тем боковые ребра трапеции являются более пологими. В предельном случае понятие «примерно» выраждается в понятие «где угодно».
Если мы оцениваем параметр качественно, например, высказавшись «Это значение параметра является средним», необходимо ввести уточняющее высказывание типа «Среднее значение . это примерно от a до b», которое есть предмет экспертной оценки (нечеткой классификации), и тогда можно использовать для моделирования нечетких классификаций трапезоидные числа. На самом деле, это самый естественной способ неуверенной классификации.
П1.6.2. Треугольные нечеткие числа Теперь для той же лингвистической переменной зададим терм-множество Т1={U приблизительно равно а}. Ясно, что а
а, причем по мере убывания до нуля степень уверенности в оценке растет до единицы. Это, с точки зрения функции принадлежности, придает последней треугольный вид (рис. П1.3), причем степень приближения характеризуется экспертом.