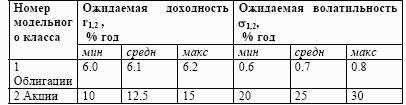
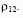Нам следовало бы еще оценить корреляцию двух индексов. Но, как я покажу
далее, в нашем случае этого не потребуется. Пока же для общности обозначим
коэффициент корреляции .
Надо сразу оговориться, что случай портфеля из двух компонент является
вырожденным с точки зрения оптимизации. Здесь полное множество
портфельных решений представляет собой участок в общем случае кривой линии
на плоскости, и он же является эффективной границей. Так что в настоящем
примере мы не сколько решаем оптимизационную задачу, сколько ищем
аналитический вид эффективной границы в координатах «риск-доходность».
Запишем (3.12) . (3.13) в частном виде
уравнение эффективной границы в виде полосы с прямолинейными границами (см.
рис. 3.4).