Оценка оптимизированной системы на данных, взятых вне пределов выборки и ни разу не использованных при оптимизации, аналогична оценке неоптимизированной системы. В обоих случаях проводится один тест без подстройки параметров. В табл. 4- 1 показано применение статистики для оценки неоптимизированной системы. Там приведены результаты проверки на данных вне пределов выборки совместно с рядом статистических показателей. Помните, что в этом тесте использованы свежие данные, которые не применялись как основа для настройки параметров системы.
Параметры торговой модели уже были определены. Образец данных для оценки вне пределов выборки охватывает период с 1.01.1995 г. По 1.01.1997 г.; модель тестировалась на этих данных и совершала смоделированные сделки. Было проведено 47 сделок. Этот набор сделок можно считать выборкой сделок, т.е. частью популяции смоделированных сделок, которые система совершила бы по данным правилам в прошлом или будущем. Здесь возникает вопрос по поводу оценки показателя средней прибыли в сделке — могло ли данное значение быть достигнуто за счет чистой случайности? Чтобы найти ответ, потребуется статистическая оценка системы.
Чтобы начать оценку системы, для начала нужно рассчитать среднее в выборке для n сделок. Среднее здесь будет просто суммой прибылей/убытков, поделенной на n (в данном случае 47). Среднее составило $974,47 нем не требуются поправки на оптимизацию или множественные тесты. Система представляет собой модель торговли индексом S&P 500, основанную на лунном цикле, и была опубликована нами ранее (Katz, McCormick, июнь 1997).
Стандартное отклонение (изменчивость показателей прибылей/убытков) рассчитывается после этого вычитанием среднего из каждого результата, что дает 47 (n) отклонений. Каждое из значений отклонения возводится в квадрат, все квадраты складываются, сумма квадратов делится на n — 1 (в данном случае 46), квадратный корень от результата и будет стандартным отклонением выборки. На основе стандартного отклонения выборки вычисляется ожидаемое стандартное отклонение прибыли в сделке: стандартное отклонение (в данном случае $6091,10) делится на квадратный корень из n. В нашем случае ожидаемое стандартное отклонение составляет $888,48.
Чтобы определить вероятность случайного происхождения наблюдаемой прибыли, проводится простая проверка по критерию Стьюдента.
Поскольку прибыльность выборки сравнивается с нулевой прибыльностью, из среднего, вычисленного выше, вычитается ноль, и результат делится на стандартное отклонение выборки для получения значения критерия t , в данном случае— 1,0968. В конце концов оценивается вероятность получения столь большого t по чистой случайности. Для этого рас-
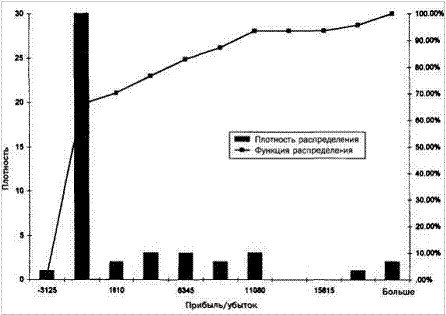
Рисунок 4- 1. функция и плотность распределения вероятностей для сделок в пределах выборки.
считывается функция распределения t для данных показателей с количеством степеней свободы, равным n— 1 (или 46).
Программа работы с таблицами Microsoft Excel имеет функцию вычисления вероятностей на основе t- распределения. В сборнике Numerical Recipes in С приведены неполные бета- функции, при помощи которых очень легко рассчитывать вероятности, основанные на различных критериях распределения, включая критерий Стьюдента. Функция распределения Стьюдента дает показатели вероятности случайного происхождения результатов системы. Поскольку в данном случае этот показатель был мал, вряд ли причиной эффективности системы была подгонка под случайные характеристики выборки. Чем меньше этот показатель, тем меньше вероятность того, что эффективность системы обусловлена случаем.
В данном случае показатель был равен 0,1392, т.е. при испытании на независимых данных неэффективная система показала бы столь же высокую, как и в тесте, прибыль только в 14% случаев.
Хотя проверка по критерию Стьюдента в этом случае рассчитывалась для прибылей/убытков, она могла быть с равным успехом применена, например, к выборке дневных прибылей. Дневные прибыли именно так использовались в тестах, описанных в последующих главах. Фактически, соотношение риска/прибыли, выраженное в процентах годовых, упоминаемое во многих таблицах и примерах представляет собой t- статистику дневных прибылей.
Кроме того, оценивался доверительный интервал вероятности выигрышной сделки. К примеру, из 47 сделок было 16 выигрышей, т.е. процент прибыльных сделок был равен 0,3404. При помощи особой обратной функции биноминального распределения мы рассчитали верхний и нижний 99%- ные пределы. Вероятность того, что процент прибыльных сделок системы в целом составит от 0,1702 до 0,5319 составляет 99%. В Excel для вычисления доверительных интервалов можно использовать функцию CRITBINOM.
Различные статистические показатели и вероятности, описанные выше, должны предоставить разработчику системы важную информацию о поведении торговой модели в случае, если соответствуют реальности предположения о нормальном распределении и независимости данных в выборке. Впрочем, чаще всего заключения, основанные на проверке по критерию Стьюдента и других статистических показателях, нарушаются; рыночные данные заметно отклоняются от нормального распределения, и сделки оказываются зависимыми друг от друга. Кроме того, выборка данных может быть непредставительной. Означает ли это, что все вышеописанное не имеет смысла? Рассмотрим примеры.
