На рис. 10- 2 изображена частота (или же период) и фазовый ответ фильтра. В этом случае середина полосы пропускания фильтра установлена на периоде 20. Кривая относительной мощности изображает мощность выходного сигнала при изменяющейся частоте входного сигнала, амплитуда которого постоянна. Фильтр пропускает сигнал максимально при частоте, соответствующей середине полосы пропускания, а при удалении от нее в обе стороны выходная мощность быстро и плавно снижается. В кривой нет вторичных пиков, и мощность выходного сигнала при значительной разнице частот падает до нуля. Фильтр никак не реагирует на появление трендов, что весьма полезно для трейдеров. Такой фильтр способен работать с данными, не очищенными от трендов и не подвергнутыми дополнительной переработке. Фазовый ответ фильтра также демонстрирует полезные характеристики. На большей части спектра ответ находится в пределах ア 90ー.
На центральной частоте фазового сдвига нет, т.е. выходной сигнал в точности синхронизован с входным, что может обеспечить идеальные входы в рынок. Как и в случае с мощностью, кривая фазового ответа плавная и гладкая — любой ученый или инженер высоко оценил бы эффективность такого фильтра. При построении подобного графика для фильтров Баттеруорта в 1997 г. результаты были гораздо менее удовлетворительными, особенно в отношении фазового ответа и задержки. При незначительном изменении периода сигнала возникали большие сдвиги по фазе, что в реальном применении разрушило бы любые попытки использовать такой фильтр для осмысленных входов в рынок.
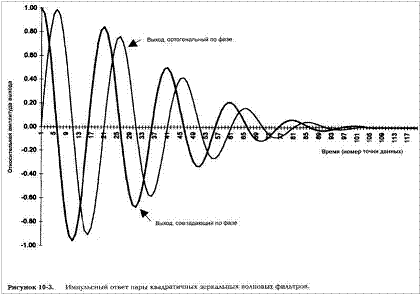
На рис. 10- 3 изображен импульсный ответ обоих выходов волнового фильтра — совпадающего по фазе с входным сигналом и ортогонального.
Эти кривые напоминают почти идеальные экспоненциально затухающие синусоиды или косинусоиды. Впрочем, затухание не совсем экспоненциально, и относительные амплитуды пиков подвергаются незаметным подстройкам для избежания влияния трендов.
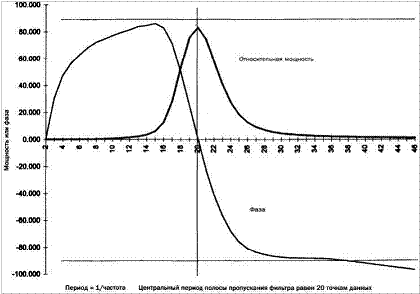
Рисунок 10- 2. Частота и фаза выходного сигнала квадратичного зеркального волнового фильтра.
В дополнение к данным, представленным на графиках, были проведены другие тесты с использованием плазмод. Плазмодой называют набор данных, подобранных так, чтобы содержать предполагаемые в реальных данных характеристики. Идея состоит в проверке того, насколько алгоритм или модель может обнаружить и проанализировать эти характеристики. Хорошая торговая система на основе циклов должна проявлять высокую эффективность на синтетической серии данных, состоящей из большого количества шума и изредка встроенных циклов. Фильтры, описанные в следующих тестах, работали в такой ситуации очень хорошо.
