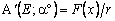Ценообразование А-опционов и их "производных" на нейтральном к риску рынке 2

и

             .

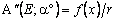Рассмотрим теперь произвольный вектор a и пусть I = {i₁, i₂,…, i_k} – множество всех тех индексов iÎT , для которых a_i = +1. Введем векторы E_I  и x_I размерности I = k как совокупности координат векторов E и x, соответствующих множеству индексов I. Отметим очевидное условие согласованности частных функций распределения F(x_I), определенных для всех подмножеств IÍT: если iÏI, то F(x_I, x_i = +¥) = F(x_I).

Используя формулы (9) и (10), можно записать следующее соотношение для стоимости "первой производной" опциона A(E, a), обобщающее соотношение (14) для произвольного вектора a:

             .

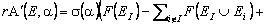
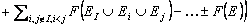Доказательство этого соотношения повторяет доказательство известного соотношения теории вероятностей для вероятности объединения событий и потому опускается. Далее, можно заметить, что знак s(a) (формула (10)) совпадает со знаком перед F(E) в последней формуле. Поэтому, меняя порядок слагаемых в ее правой части на обратный, получаем иное представление:

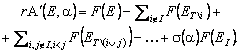                                                                                                                                             (3)