Пусть задана иерархия критериев и альтернатив (рис. 2.3.) и для каждого уровня определен индекс однородности и векторы приоритетов критериев следующим образом:
ИО1 — индекс однородности для 1-го уровня;
{ИО2, ИО3} — индексы однородности для 2-го уровня;
{ИО4, ИО5, ИО6} — индексы однородности для 3-го уровня;
{W1} — вектор приоритетов критериев К2 и К3 относительно критерия К1;
{W2},{W3} — векторы приоритетов критериев К4, К5, К6 относительно критериев К2 и К3 второго уровня.
В этом случае индекс однородности рассматриваемой иерархии можно определить по формуле
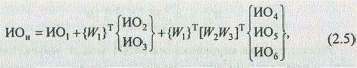
где Т — знак транспонирования.
Определение отношения однородности ООИ для всей иерархии осуществляется по формуле
ООИ = ИОИ / М(ИОИ),
где М(ИОИ) — индекс однородности иерархии при случайном заполнении матриц попарных сравнений.
