Сторона АВ квадрата ABCD на рисунке 1.4 делится пополам. Чертится дуга круга с центром в точке Е и радиусом ЕС, отсекающая продление АВ в точке F. Перпендикулярно AF чертится линия FG, пресекающая продление DC в точке G. AFGD — золотой прямоугольник. Согласно формальному определению, геометрическое представление золотого сечения в прямоугольнике означает, что длина прямоугольника этой формы в 1,618 раз больше, чем его ширина. И вновь появляется отношение Фибоначчи ФИ, на сей раз в пропорциях золотого прямоугольника.
Держа в уме представление отношения Фибоначчи ФИ в одномерной (линия) и двумерной (прямоугольник) геометрии, можно перейти к более сложным геометрическим объектам. Они подведут ближе к инструментам, которые мы хотим применять для анализа параметров времени и цены фондовых и фьючерсных рынков.
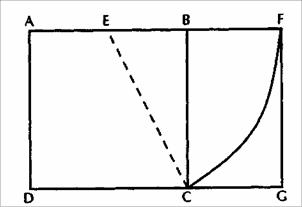
Рисунок 1.4 Золотое сечение прямоугольника. Источник: FAM Research, 2000.
Единственной математической кривой следующей модели естественного роста является спираль, выраженная в таких природных феноменах, как Spira mirabilis или раковина наутилуса. ФИ-спираль называют самой красивой математической кривой. Этот тип спирали часто встречается в природе. Ряд суммирования Фибоначчи и золотое сечение, представленное выше как его геометрический эквивалент, очень хорошо ассоциируются с этой замечательной кривой.
На рисунке 1.5 показана рентгенограмма раковины камерного наутилуса ("кораблика"). Последовательные камеры наутилуса построены, следуя форме ФИ-спирали. По мере роста раковины размер камер увеличивается, но их форма остается неизменной.
Для демонстрации геометрии ФИ-спирали лучше всего использовать золотой прямоугольник как основание для геометрического анализа. Это показано схематично на рисунке 1.6.
мЮВЮКН

