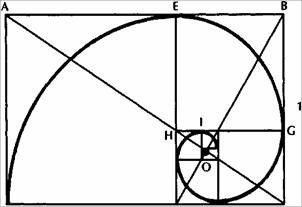
Частное от деления длины на высоту прямоугольника ABCD на рисунке 1.6 можно вычислить. Как мы узнали ранее, оно составляет АВ-г-ВС = ФИ-Н = 1,618. Через точку Е, также называемую золотым сечением АВ, проводится линия EF, перпендикулярная АВ, отрезающая от прямоугольника квадрат AEFD. Остающийся прямоугольник EBCF — золотой прямоугольник. Если отделить квадрат EBGH, то остающаяся фигура HGCF также будет золотым прямоугольником. Этот процесс можно повторять неопределенно долго, пока конечный прямоугольник О не станет настолько маленьким, что будет неотличим от точки.
Конечная точка О называется полюсом равноугольной спирали, которая проходит через золотые сечения D, Е, G, J и так далее.

Рисунок 1.5 ФИ-спираль, представленная в раковине наутилуса.
D F J С
Рисунок 1.6 Геометрия ФИ-спирали. Источник: FAM Research, 2000.
Стороны прямоугольника почти, но не полностью касательные кривой.
Отношение ФИ-спирали кряду Фибоначчи очевидно из рисунка 1.6, потому что ФИ-спираль проходит по диагонали через противоположные углы последовательных квадратов, например, DE, EG, GJ и так далее. Длины сторон этих квадратов формируют ряд Фибоначчи. Если самый маленький квадрат имеет сторону длиной d, смежный квадрат должен также иметь сторону длиной d. Следующий квадрат имеет сторону длиной 2d (вдвое длиннее d), следующий 3d (втрое длиннее d), формируя ряд Id, 2d, 3d, 5d, 8d, 13d... который является хорошо известной последовательностью Фибоначчи: 1—1—2—3—5—8—3— и так далее до бесконечности.
Спираль не имеет конечной точки. При бесконечном росте наружу (или внутрь) ее форма остается неизменной. Два сегмента спирали идентичны по форме, но отличаются по размеру точно на коэффициент ФИ. Все спирали, чьи темпы роста являются элементами ряда ФИ 0,618-1,000-1,618-2,618-4,236-6,854-11,090-и так далее, будут в контексте этой книги называться ФИ-спира-лями.
ФИ-спираль — связующее звено между рядом суммирования Фибоначчи, вытекающим из него отношением Фибоначчи ФИ, и волшебством природы, которое мы видим вокруг нас.
