Транспортный и рабочие пункты и изодапаны
Он сделал существенный шаг впред по сравнению с Й. Тюненом и В. Лаунхардтом, введя в теоретический анализ новые факторы размещения производства в дополнение к транспортным издержкам и ставя более общую оптимизационную задачу: минимизацию общих издержек производства, а не только транспортных. А. Вебер создал подробную классификацию факторов размещения по их влиянию, степени общности и проявлениям. Фактором размещения он называет экономическую выгоду, которая выявляется для хозяйственной деятельности в зависимости от места, где осуществляется эта деятельность. Эта выгода заключается в сокращении издержек по производству и сбыту определенного промышленного продукта и означает, следовательно, возможность изготовлять данный продукт в одном каком-либо месте меньшими издержками, чем в другом месте. В результате отсеивания элементов производственных издержек, не зависящих от местоположения, А. Вебер оставляет три фактора: издержки на сырые материалы, издержки на рабочую силу и транспортные издержки. Однако первый из них — разницу в ценах на используемые материалы — можно, как считает Вебер, выразить в различиях транспортных издержек, исключив из самостоятельного анализа.
Все остальные условия, включающие размещение предприятия, он рассматривает как некоторую объединенную агломерационную силу, или третий штандортный фактор. Таким образом, в конечном счете анализируются три фактора: транспорт, рабочая сила и агломерация.
Дальнейший анализ ведется последовательно по трем факторам. Соответственно выделяются и три основные ориентации в размещении: транспортная, рабочая и агломерационная.
Транспортная ориентация. Согласно Веберу, величина транспортных издержек зависит от веса перевозимых грузов и расстояния перевозки. Под влиянием транспортных издержек промышленное предприятие будет притягиваться к тому пункту, в котором с учетом местоположения потребительского центра и источников сырья транспортные издержки минимальны. Этот пункт есть транспортный штандорт (транспортный пункт). Для его нахождения используется весовой (локационный) треугольник В. Лаунхардта.
При этом важную роль играют два показателя: материальный индекс и штандортный вес.
Например, для производства 100 т продукта требуется 300 т одного материала и 200 т другого. Тогда материальный индекс будет равен (300 + 200) : 100 = 5. Штандортный вес составит 300 + 200 + 100 = 600 (т), или 6 в пересчете на 1т готового продукта, т.е. штандортный вес равен материальному индексу плюс единица. Существуют производства, у которых материальный индекс меньше единицы.
Исходя из соотношения указанных показателей легко установить, что производства с высоким материальным индексом тяготеют к пунктам производства сырья материалов, а производства с небольшим индексом к центру потребления.
Рабочая ориентация. Далее, учитывая различия в издержках на рабочую силу (рабочих издержек), определяется рабочий пункт, т.е. пункт с наименьшими рабочими издержками. Рабочий пункт будет притягивать производство к себе, в результате чего производство либо останется в транспортном пункте, либо переместится в рабочий пункт.
Такое перемещение может произойти тогда, когда экономия на рабочих издержках в данном пункте перекрывает перерасход в транспортных затратах из-за перемещения производства.
Для определения промышленного штандорта с учетом совместного влияния факторов транспортных издержек и рабочей силы А. Вебер прибегает к построениям так называемых изодапан (isodapane), смысл которых заключается в следующем. Приросты транспортных затрат, обусловленные перемещением производства из транспортного пункта в рабочий, увеличиваются с удалением от транспортного пункта, причем более или менее равномерно в любом направлении удаления. Поэтому в каждом направлении должны существовать пункты, для которых приросты транспортных затрат (или издержки отклонения) будут одинаковыми.
Линии, соединяющие эти пункты одинаковых издержек отклонения, и называются изодапанами.
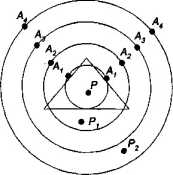
Рис. 3.3. Транспортный и рабочие пункты и изодапаны
Графически (рис. 3.3) такие линии можно представить в виде замкнутых кривых, которые описываются вокруг пункта транспортного минимума (Р) и соединяются точки одинаковых отклонений в транспортных издержках при перемещении пpoизводства в рабочие пункты (P1 или P2). При этом изодапана, соединяющая точки, в которых отклонения транспортных издержек равны экономии на рабочих издержках, называется критической изодапаной для данного рабочего пункта.
Если данный рабочий пункт лежит внутри своей критической изодапаны, то перемещение производства из транспортного пункта в рабочий пункт выгодно, а если вне ее, то перемещение невыгодно. Например, если для рабочего пункта P1 критической изодапаной является А3, то предприятие предпочтительнее разместить в транспортном пункте Р. Если критической изодапаной является А4, то предприятие целесообразно разместить в рабочем пункте P1.
Агломерационная ориентация. Анализ влияния агломерационных факторов на размещение промышленного предприятия Вебер провел на базе оценки изменений, вызываемых процессами агломерации, в оптимальной схеме размещения производства, полученной на основе транспортной и рабочей ориентаций. Для этого он ввел дополнительное понятие — индекс сбережений.
Смысл того понятия поясним на следующем простом примере.
Пусть различным объемам агломерированной массы (например, годовым выпускам продукции) соответствуют различные удельные издержки:
1) 100 т — 10 руб.;
2) 400 т — 6 руб.;
3) 1600 т — 4руб.;
4) 6400 т — 3 руб.
Уменьшение удельных издержек при росте объема производства отражает эффект концентрации. Разница в издержках для агломерированных масс по сравнению с первым уровнем концентрации производства составит: для второго уровня — 4(10 - 6); для третьего — 6(10 - 4); для четвертого — 7(10 - 3). Полученные величины (4; 6; 7) и представляют собой те сбережения, которые получаются для различных степеней агломерации и повышаются при укрупнении производства.
Эти величины Вебер и называл индексами сбережений при агломерации.
Проводимый анализ влияния фактора агломерации на размещение производства предполагает отсутствие влияния всех других факторов, кроме транспортного. Исходя из транспортной ориентации отыскиваются отклонения производства транспортных пунктов, обусловленные действием фактора агломерации. Такие отклонения целесообразны, если издержки отклонения перекрываются сбережениями в агломерационных пунктах.
Дни определения места размещения агломерационного производства вокруг транспортных пунктов проводятся изодапаны, среди которых выделяется критическая изодапана, т.е. геометрическое место точек, где перерасход транспортных затрат равен экономии от агломерации производства. Вебер утверждает, что отклонение изолированных производств от транспортных пунктов имеет смысл только тогда, когда все отклоняющиеся производства, не выходя за пределы своих критических изодапан, соединятся в каком-то одном месте. Таким местом является площадь общего сегмента, образованного пересекающимися критическими изодапанами, так как только внутри этого сегмента издержки отклонения для каждого производства не превышают той выгоды, которая получается от соединения, т.е. не превышает агломерационных сбережений.
Иллюстрацией этого рассуждения является рис. 3.4.
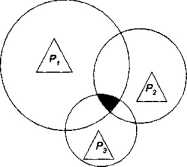
Рис. 3.4. Транспортные пункты
и площадь агломерации производств
Агломерируемые производства должны размещаться в штрихованном сегменте. Выбор точки размещения происходит с учетом транспортного фактора. В более общем случае несколько предприятий образуют не один, а несколько сегментов.
А. Вебер рассматривает различные ситуации при осуществлении агломерации, конкретизируя методику нахождения штандорта. Он предлагает формулы агломерационных эффектов.
Пусть М — производственная масса какого-либо крупного производства. Величина сбережений от агломерации в расчете на единицу продукта будет выражаться в виде функции сбережения — f(M). Тогда общая величина сбережений на всю производственную массу составит:
Э1 = М • f(M).
Допустим, что с крупным производством сливается мелкое производство с производственной массой т. Тогда общая сумма сбережения для двух производств составит:
Э2 = (М + т) • f(M + т).
Определим приращение сбережения, получаемого в результате слияния двух производств:
Э = Э2 Э1 = (М + т) • f(M + т) M • f(M)
Cлияние мелкого производства с крупным происходит, согласно А. Веберу, в том случае, если величина сбережения от слияния предприятий больше (или по крайней мере не меньше) перерасхода транспортных затрат из-за переноса производства т в пункт производства М, т.е.:
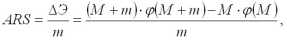
где А — штандортный вес;
R — радиус отклонения;
S —ставка транспортного тарифа (т/км)
Отсюда можно определить величину наибольшего, экономики допустимого, радиуса отклонения.
Определяем первую производную функции:
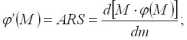
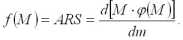
Функция f(M), называемая функцией агломерации, служит выражением притягательной силы крупного производства по отношению к рассеянным мелким производствам. Поскольку f(M) = ARS, то R = f(M) : AS, т.е. максимально допустимый радиус отклонения прямо пропорционален функции агломерации и обратно пропорционален штандортному весу и тарифной ставке.
- Теория центральных мест
- Множество вариантов обмена.
- Теоретические разработки о пространственной организации хозяйства
- Принципы и факторы размещения производительных сил региона
- Совет по изучению производительных сил
