Теория центральных мест


Выведенная формула агломерации f(M) = ARS включает три фактора, от которых зависит агломерация. Требуется учесть еще одно условие — производственную плотность.
Обозначим через р производственную плотность, под которой здесь понимается объем продукции, приходящейся на единицу площади с радиусом R, при равномерном распределении производства на данной площади. Тогда вся производственная масса, притягиваемая к агломерационному центру, будет равна R2p = М.
Отсюда


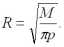
Сравнивая полученную формулу с ранее выведенной, получаем окончательную формулу агломерации



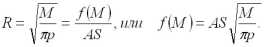
А. Веберу первому удалось выработать многофакторную теорию размещения промышленного предприятия, опирающуюся на методы количественного анализа (математическое моделирование). Так же как и его предшественник В. Лаунхардт, А. Вебер не вышел за рамки проблемы размещения отдельного предприятия. Однако его исследования стали мощным стимулом для создания более общих теорий размещения.

3.4. Теория центральных мест
Первую теорию о функциях размещения системы населенных пунктов (центральных мест) в рыночном пространстве выдвинул В. Кристаллер в своем труде Центральные места в южной Германии, опубликованном в 1993 г. Теоретические выводы он обосновал эмпирическими данными.
Центральными местами В. Кристаллер называет экономи_еские центры, которые обслуживают товарами и услугами не только себя, но и население своей округи (зоны сбыта). Согласно В. Кристаллеру, зоны обслуживания и сбыта с течением времени имеют тенденцию оформляться в правильные шестиугольники (пчелиные соты), а вся заселенная территория покрывается шестиугольниками без просветов (кристаллеровская решетка). Благодаря этому минимизируется среднее расстояние для сбыта продукции или поездок в центры для покупок и обслуживания.
Теория В. Кристаллера объясняет, почему одни товары и услуги должны производиться (предоставляться) в каждом населенном пункте (продукты первой необходимости), другие — средних поселениях (обычная одежда, основные бытовые услуга и т.п.), третьи — только в крупных городах (предметы роскоши, театры, музеи и т.д.)
Каждое центральное место имеет тем большую зону сбыта, чем выше уровень иерархии, к которому оно принадлежит. Кроме продукции, необходимой для зоны своего ранга (своего шестиугольника), центр производит (предоставляет) товары и услуги, типичные для всех центров низших рангов.




Рис. 3.5. Размещение зон обслуживания
и населенных пунктов по теории В. Кристаллера

Тип иерархии определяется числом центральных мест данного уровня. Число подчиненных центральных мест, увеличенное на единицу, обозначается буквой К. Любой центр всегда имеет зависимое от него одинаковое количество поселений, занимающих более низкую ступень.
Рассмотрим, например, случай, когда имеется трехступенчатая иерархия поселений: город — поселок — деревня. Тогда при К = 7 вокруг каждого города будет расположено 6 поселков, а вокруг каждого поселка — 6 деревень, т.е. вокруг города будет всего 6 поселков и 36 деревень. При четырехступенчатой иерархии (город — поселок — поселение — деревня) вокруг города разместятся 6 поселков, 36 поселений и 216 деревень и т.д. Общая формула для отражения данной зависимости имеет следующий вид:


Mn =(K 1)n ,
где Mn — число зависимых мест на той или иной степени иерархии;
п — ступень иерархии.
Количество возможных типов иерархии в принципе может быть любым. Однако наибольшее внимание В. Кристаллер и его последователи уделяли анализу трех типов, или вариантов, иерархии при К = 3, 4, 7. Эти варианты иерархии систем расселения интерпретируются следующим образом.
Вариант при К = 3 обеспечивает оптимальную конфигурацию рыночных зон (территорий, население которых приобретает товары и услуги в данном центральном месте). Обслуживание территории достигается наименьшим возможным числом центральных мест. При этом каждое центральное место обслуживается тремя центральными местами следующего, более высокого уровня иерархии и находится на равных расстояниях от них.
Вариант при К = 4 создает наилучшие условия для строительства транспортных путей, так как в этом случае наибольшее число центральных мест будет расположено на одной трассе, соединяющей более крупные города, что обеспечит минимальные издержки на строительство дороги, т.е. данное центральное место будет находиться на кратчайшем расстоянии до двух ближайших центров более высокого уровня иерархии.


Вариант при К = 7 представляется целесообразным, если необходим четкий административный контроль. В этом случае все центральные места, зависимые от данного места, полностью входят в его зону.
Из приведенных примеров видно, что функции поселений различны, каждое их них имеет свой радиус влияния и притяжения. В соответствии с этим возможны и разные способы территориальной организации систем расселения, при которых создаются наиболее благоприятные условия для выполнения тех или иных их функций. Рассмотренные три случая, соответствующие значениям показателя К, можно интерпретировать как рыночную, транспортную и административную ориентации в формировании территориальной структуры расселения.
Теория центральных мест В. Кристаллера хотя и носит крайне абстрактный характер, но позволяет сформулировать общие представления о целесообразном расселении на той или иной территории. Ее можно рассматривать как теорию, дающую идеальный эталон системы расселения, с которым следует сравнить складывающиеся в реальности системы расселения с целью выявления направлений их совершенствования. Известны также примеры практического применения теории центральных мест к решению конкретных проблем территориальной организации хозяйства и расселения в различных странах.

3.5. Региональные рынки и пространственная теория цены
Многие учебники микроэкономики начинаются с анализ механизма спроса и предложения на товарном рынке, демонстрируя при этом модель рыночного равновесия, где предполагается, что спрос на товар D падает при увеличении цены Р, предложение товара S, наоборот, растет при увеличении цены (рис. 3.6). Пересечение обратных функций спроса и предложения QD = D(P) и QS = S(P) дает точку равновесия спроса и предложения Q* и цену равновесия Р*:
Q* = D (Р*) = S (Р*).
Приведенная широко известная модель имеет, однако, принципиальный недостаток: она игнорирует влияние пространства или (что по сути то же самое) допускает, что рынок является точкой. Для теории пространственной или региональной экономики такие предположения неприемлемы. По-видимому, первым, кто обратил внимание на это несоответствие (еще в 1838 г.), был французский экономист — математик О. Курно.
Начальный шаг анализа механизма спроса и предложения в экономическом пространстве — это рассмотрение пространственно разделенных автономных региональных рынков. Очевидно, что в каждом полностью автономном регионе будут устанавливаться свое рыночное равновесие спроса и предложения и свои цены рыночного равновесия, т.е. в каждом регионе описанная выше модель будет работать автономно.
Ситуация принципиально усложняется, если региональные рынки связываются друг с другом. Проведем анализ двух рынков региональной системы, производящей и потребляющей однородный товар.



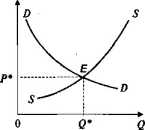
Рис. 3.6. Равновесие спроса и предложения
однородного товара на точечном рынке

Пусть А1 — цена равновесия для автономного региона 1; А2 — то же для автономного региона 2; Т1,2 — транспортные затраты на доставку единицы товара из региона 1 в регион 2; Т2,1— транспортные затраты на доставку единицы товара из региона 2 в регион 1. Задача состоит в том, чтобы определить объемы производства, межрегиональные поставки товара и цены равновесия (Р1* и Р2*) в системе связанных региональных рынков.
Пусть для определенности А2 А1. Тогда у производителей (продавцов) возникает стимул для поставки товара из региона 1 в регион 2 с целью реализации его по более высокой цене. Последствие открытия региональных рынков будет зависеть от соотношения разницы А2 — А1 и транспортных затрат Т1,2 .
Если оказывается, что А2 — А1 Т1,2 , то межрегиональная торговля неэффективна, поскольку выигрыш производителя (продавца) региона 1 на цене реализуемого товара меньше транспортных затрат. В этом случае состояние равновесия региональных рынков сохраняются такими же, как и при автономном их функционировании. Более интересен вариант, когда А1 = А2 . Тогда выгодно поставлять товар из региона 1 в регион 2, а на каждом региональном рынке установится новое равновесие. Цены равновесия будут удовлетворять условию Р2* = Р1* + Т1,2 (причем Р1* А1; Р2* А2) , а вывоз товара из региона 1 в регион 2 будет равен ввозу товара в регион 2 из региона 1 (с обратным знаком):
E1,2 = E2,1 .
Выведение условий рыночного равновесия для многорегиональной системы представляет собой принципиально более сложную математическую задачу. До создания мощных компьютеров и алгоритмов нахождения состояния равновесия в задачах большей размерности предпринимались попытки моделирования решений с помощью особых методик. В настоящее время решение таких задач не представляет чрезмерной сложности.

3.6. Теории региональной специализации



Содержание раздела