В качестве главного практического доказательства информационно-эффективного поведения финансовых рынков обычно приводят факт некоррелированности последовательных ценовых приращений, зафиксированный в ряде исследований финансовых инструментов развитых рынков. В этой связи необходимо упомянуть тесно связанную с гипотезой эффективного рынка так называемую теорию случайных блужданий цен.
Согласно «теории случайных блужданий» цена финансового актива вследствие случайного характера поступающей информации и эффективности рынков следует случайным независимым друг от друга изменениям. Каждое изменение цены не зависит от предыдущих изменений и, соответственно, не оказывает влияния на последующие. В этом случае будущее ожидаемое значение цены равно ее текущему значению. Кроме того, в модели «случайных блужданий» предполагается, что каждое изменение цены подчиняется одному и тому же распределению вероятностей с одинаковыми параметрами — такими, как математическое ожидание и дисперсия, причем математическое ожидание ценовых изменений принимается равным нулю.
Определенный таким образом процесс «случайного блуждании» обладает, во-первых, свойством Маркова и, во-вторых, мар-тингальным свойством. Говорят, что случайный процесс обладает свойством Маркова, если вся информация, необходимая для определения условной вероятности будущего значения случайной величины, содержится исключительно в текущем значении этой величины (а не в историческом распределении вероятностей). Для «случайных блужданий» это следует из предположения независимости приращений цен. Каждое из будущих приращений не зависит ни от предыдущих изменений, ни от текущего абсолютного значения цены, однако будущее значение цены зависит от текущего ценового уровня.
Мартингалъное свойство предполагает, что условное ожидание будущего значения случайной переменной равно ее текущему значению. Это условие также выполняется для «случайных блужданий», поскольку все изменения цен имеют нулевое математическое ожидание.
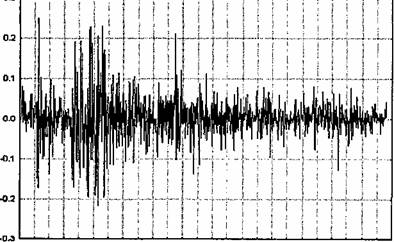
Рис. 1.1. Приращения за день логарифмов цен акций компании Cadburry Schweppes PLC
Здесь необходимо отметить, что мартингал — более общий стохастический процесс, чем «случайные блуждания», поскольку мартингальное свойство не требует обязательного постоянства дисперсии, а также независимости приращений случайной переменной. Методами стохастической финансовой математики можно показать, что если поведение цен на финансовом рынке как случайный процесс обладает мартингальным свойством, то арбитраж на таких рынках невозможен, а следовательно, данный рынок является полностью эффективным и использование предыдущей рыночной информации (т.е. технический анализ) не даст никаких практических результатов. С другой стороны, процессы изменения цен на эффективных рынках должны быть мартингалами, поскольку рыночная эффективность предполагает полную независимость ценовых приращений. Мартингапьность, как и эффективность рынков, означает бесполезность методов технического анализа, а следовательно, статистические исследования реальных рыночных цен имеют большое значение для оценки возможности применения методов, которые будут описаны в настоящем пособии.
