Последствия этого открытия были революционными. Представьте себе, что поверхность Земли покрыта сетью метеостанций с трехдесятичной точностью, находящихся только в 30 см друг от друга, посылающих свои измерения в центральный компьютер каждую минуту. И предположите, что этот компьютер достаточно большой, чтобы вместить в себя совершенно правильную модель глобальных погодных моделей. Если бы даже и было так, то надежный прогноз погоды на месяц вперед сделать просто невозможно. Как раз вопреки своим первоначальным намерениям и ко всеобщему удивлению, Лоренц смог доказать, что невозможно и никогда не будет возможно давать долгосрочные прогнозы погоды.
Эффект бабочки — один из элементов системы математических феноменов, с тех пор обобщенно названных термином "детерминированный хаос". Этот феномен охарактеризован Чера Л. Сайерсом следующим образом (1989): "Процесс характеризуется детерминированным хаосом, если он генерирован полностью детерминированной системой1, возникающей как результат беспорядочно функционирующих рядов в стандартных временных диапазонах". Нас окружает хаос. Представим себе дымок сигареты в тихой комнате. Тысячи микроскопических частиц дыма поднимаются узкой колонкой, подталкиваемые горячим воздушным потоком. Затем внезапно колонка прерывается, заменившись турбулентными, постоянно меняющимися завихрениями дыма. Линейный поток трансформировался в хаос. И это происходит независимо от того, где вы находитесь. Или рассмотрим игру в футбол. Ни один, даже самый проницательный эксперт не сможет предугадать, где мяч окажется всего лишь через 10 секунд.
Хаос наступает главным образом в отношениях, где присутствуют самопроизвольные усиливающиеся механизмы. Вообразите себе систему, в которой событие "А" приводит к событию "В", а событие "В" к событию "С". Если событие "С" затем воспроизводит событие "А", тогда в этом процессе есть простая цепь положительной обратной связи.
Если мы попытаемся наметить в общих чертах взаимоотношения в экономике страны, как если бы это была метеорология, то вскоре столкнемся со сложными вариантами этих механизмов. Среди хорошо известных примеров есть так называемые эффекты мультипликации и акселерации, тезаврирование, самопроизвольное усиление ожиданий роста ("держаться наравне с Джонесесом"), увеличение потребностей в капитале изза смещений во взаимоотношениях труда и капитала и т. д., — все вместе эти многочисленные цепочки обратных связей могут означать, что системы имеют не просто равновесие, а сами себя раскачивают или демонстрируют иные сложные движения. Каждая
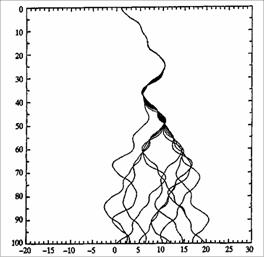
Рисунок 4 Эффект бабочки. График показывает математическое моделирование 11 объектов, скользящих вниз с неравномерными наклонами пиков и впадин, расположенных в синусоидальной модели. Длина наклона 100 метров. При моделировании объекты стартуют с одинаковым распределением точек, отдаленных друг от друга по горизонтали на 5 мм. Приблизительно через 30 метров их распределение уже в 20 метрах друг от друга. Интересный момент: график напоминает сигаретный дым, если его перевернуть наоборот. (Источник: Эдвард Н. Лоренц, Центр Метеорологии и Физической Океанографии, Кембридж, Массачусетс.)
из этих положительно воздействующих цепей обратных связей может вносить свой вклад в самопроизвольно усиливающую природу экономического феномена, пока окончательно не будет заторможена другими механизмами. Чтобы правильно описать эти системы, необходимо применить нелинейную математику.
