В отсутствие непосредственной информации о распределении вероятностей будущих цен базового актива для его оценки можно использовать сами рыночные цены опционов. Как уже отмечалось, из теоретических соображений эти цены должны быть согласованы. Остановимся на этом подробнее и введем необходимые определения по аналогии с однопериодным случаем.
Итак, предположим, что на теоретическом n-периодном рынке для любой пары векторов (E; a) котируются A-опционы A(E, a) (хотя бы один из них). Введем наведенную рынком (точнее, ценами зависящих от пути опционов) совместную плотность вероятности fm(x), x = (x1, x2,…, xn), для цен базового актива в моменты времени t = 1, 2 ,…, n, определяемую равенством
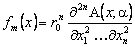 ,
,
где A(E; a) = A(E; a) – цена A-опциона с параметрами (E; a), а коэффициент
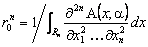
вновь, как и в однопериодном случае, интерпретируется как наведенный рынком безрисковый относительный доход с тем уточнением, что теперь этот относительный доход приходится на весь горизонт инвестирования – n периодов.
Введенные определения корректны. Действительно, поскольку A"(E, a) = D(E), а платежная функция инструментов D(E) при всех EÎRn неотрицательна, то из условия недопущения арбитража A"(E; a) ³ 0, EÎRn, и потому fm(x) ³ 0. Нормировочный коэффициент делает интеграл от функции fm(x) по пространству Rn равным 1.



