Теперь увеличим число используемых ближайших соседей до двух. На этот раз метод k-ближайших соседей не сможет классифицировать отклик точки запроса, поскольку вторая ближайшая точка имеет знак минус и оба знака равноценны (т.е. победа с одинаковым количеством голосов).
Далее увеличим число используемых ближайших соседей до 5. Таким образом, будет определена целая окрестность точки запроса (на графике ее граница отмечена красной( серой) окружностью). Так как в области содержится 2 точки со знаком "+" и 3 точки со знаком "-" , алгоритм k-ближайших соседей присвоит знак "-" отклику точки запроса.
Далее рассмотрим принцип работы метода k-ближайших соседей для решения задачи регрессии. Регрессионные задачи связаны с прогнозированием значения зависимой переменной по значениям независимых переменных набора данных.
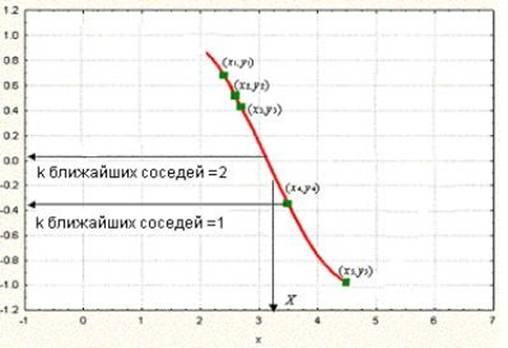
Рассмотрим график, показанный на рис. 10.6. Изображенный на ней набор точек (зеленые прямоугольники) получен по связи между независимой переменной x и зависимой переменной y (кривая красного цвета). Задан набор зеленых объектов (т.е. набор примеров); мы используем метод k-ближайших соседей для предсказания выхода точки запроса X по данному набору примеров (зеленые прямоугольники).