Отметьте, что ковариация ценной бумаги самой к себе является дисперсией, так как коэффициент линейной корреляции ценной бумаги самой к себе равен 1:
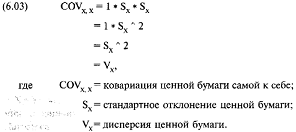
Теперь можно создать таблицу ковариаций для нашего примера с четырьмя инвестиционными альтернативами:
Т I L S
Т 0,1 - 0,0237 0,01 0
I - 0,0237 0,25 0,079 0
L 0,01 0,079 0,4 0
S 0 0 0 0
Мы собрали необходимую параметрическую информацию и теперь попытаемся сформулировать основную проблему. Во-первых, сумма весов ценных бумаг, составляющих портфель, должна быть равна 1, так как операции ведутся на денежном счете, и каждая ценная бумага полностью оплачена:
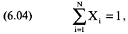
где N == число ценных бумаг, составляющих портфель;
Х = процентный вес ценной бумаги L
Важно отметить, что в уравнении (6.04) каждое значение Х должно быть неотрицательным числом.
