Обозначим среднее арифметическое HPR переменной А, а среднее геометрическое HPR переменной G. Используя уравнение (1.166), мы можем выразить оценочное среднее геометрическое следующим образом:
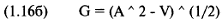
Из этого уравнения получим:
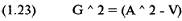
Теперь вместо дисперсии подставим стандартное отклонение [как в (1.16а)]:
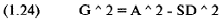
Из этого уравнения мы можем выделить каждую переменную, а также выделить ноль, чтобы получить фундаментальные соотношения между средним арифметическим, средним геометрическим и разбросом, выраженным здесь как SD ^ 2:
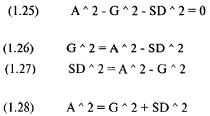
В этих уравнениях значение SD^2 можно записать как V или как (1,25 * М) ^2. Это подводит нас к той точке, когда мы можем описать существующие взаимосвязи.
мЮВЮКН

