В важном частном случае, когда хеджирование отсутствует,
zP = 0, v0 = -1/T,
К = 0, и распределение H(v0 , v1) сходится к обыкновенному нормальному виду, если распределение цены подлежащего актива нормально. При нулевой дисперсии эта нормальная плотность распределения вырождается в дельта-функцию, что соответствует определенной доходности безрискового актива. Таким образом, классические распределения доходности активов являются вырожденными частными случаями более сложного распределения H(v0 , v1)-вида.
Можем ли мы, зная распределения доходности отдельных хеджированных активов, получить распределение доходности модельного портфеля на их основе аналитическим путем? К величайшему сожалению, нет. Математическая теория композиции вероятностных распределений свидетельствует о том, что сумма двух стохастически зависимых случайных величин с усеченно-нормальным распределением есть случайная величина, не обладающая усеченно-нормальным распределением. В результирующем вероятностном распределении такой величины плотность является мультимодальной функцией. Все это говорит о том, что точному аналитическому решению задача оптимизации модельного портфеля с хеджированными активами не поддается.
В качестве альтернативы можно предолжить для оптимизации хеджированного модельный портфеля схему минимизации уровня предельных потерь. Действительно, по каждому хеджированному активу известна минимальная доходность v0i. Соответственно, минимальная доходность по портфелю составляет
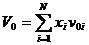
где хi – доли компонент в портфеле.
Максимизируя V0, мы решаем задачу нелинейной оптимизции относительно не только оптимального распределения долей активов, но и глубины их хеджирования, а также соотношения страйков по put-опционам и размеров опционных премий.
Оптимизация функционала (3.29) не является оптимизацией модельного портфеля в постановке Марковица уже потому, что в качестве ограничения в задаче оптимизации здесь не выступает риск портфеля. Чтобы учесть параметры риска в оптимизации, можно перед решением задачи (3.29) решить классическую задачу Марковица, а в задаче (3.29) оптимизировать уже только параметры хеджирования, зафиксировав веса компонент. Такой компромисс позволяет избежать применения статистического моделирования портфеля в духе Монте-Карло, которое я лично считаю недопустимой методикой для оптимизации фондового портфеля.
