Пико образная эмпирическая плотность распределений хорошо видна на рис. 1.4, 1.5 и 1.6, а тяжелые «хвосты» отчетливо проявляются на графиках эмпирических функций распределения, построенных в нормальном масштабе (рис. 1.7, 1.8 и 1.9). Нормальный масштаб означает, что ось ординат на этих графиках оцифрована следующим образом: вместо вероятности, равной F(Z), где F— функция Лапласа, подписывается значение Z. В таком масштабе нормальное распределение выглядит в виде прямой линии
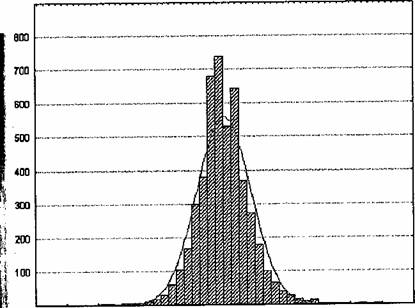
-0.10 -0.08 -0.06 -0.04 -0,02 0.00 0.02 0.04 0.06 0.08 0.10 0.12
Рис. 1.4. Эмпирическая плотность распределения приращений
за день логарифмов цен акций компании Cadburry Schweppes PLC
и соответствующая нормальная плотность (сплошная линия)
Необходимо также отметить, что наблюдаемая для ряда финансовых активов некоррелированность приращений цен еще не означает их независимости. Более того, экспериментально зафиксированы факты положительной корреляции значений, являющихся квадратами и абсолютными величинами ценовых приращений.
Как абсолютная эффективность рынков, так и их полная иррациональность являются противоположными идеальными положениями на реальных рынках. В действительности различные финансовые рынки обладают различной степенью эффективности, и оценка эффективности этих рынков представляет собой одну из важных задач биржевых аналитиков.
