Отношения различных членов ряда Фибоначчи называются соотношениями Фибоначчи. Последовательность Фибоначчи и соотношение ф, называемое также «золотым» соотношением, обладают рядом исключительно важных математических свойств. В частности, при прибавлении к ф единицы получается число, обратное ф (1 + ф = = 1/ф), а если из единицы вычесть ф, то получится отношение чисел Фибоначчи, разделенных одним членом последовательности (0,382) и многие другие. Замечено, что соотношения Фибоначчи часто встречаются в строении природных объектов, произведений музыки, архитектуры, живописи и пр.
Рис. 6.18. Комбинация коррективных волн
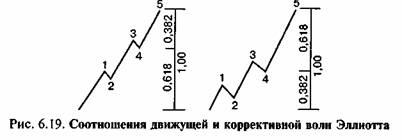
Последователи Эллиотта, основываясь на собственных наблюдениях, полагают, что соотношения Фибоначчи также могут проявляться при анализе движений цен на финансовых рынках. В рамках волновой теории анализируются, во-первых, соотношение размера коррекции и предшествующего ей основного движения и, во-вторых, соотношения однонаправленных волн внутри более крупной волновой модели. Считается, что для пропорции между амплитудой коррективной волны и предыдущего импульса часто характерна величина, близкая к «золотому» соотношению, т.е. к значению 61,8%. Также возможна коррекция на 50% основного движения. «Боковые» коррекции часто совершают возврат цен на величину, близкую к другому соотношению Фибоначчи — 38,2% (рис. 6.19).