Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью
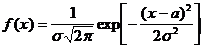
Нормальное распределение определяется двумя параметрами: математическим ожиданием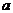 
и средним квадратическим отклонением
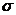и на графике представляет собой симметричную колоколообразную кривую Гаусса, имеющую максимум в точке, соответствующей значению 
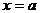, а при 
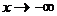и 
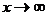асимптотически приближающуюся к оси абсцисс. Точка перегиба кривой находится на расстоянии 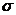от центра распределения. Изменение параметра 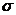приводит к изменению степени растяжения кривой: с уменьшением 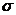кривая вытягивается в центре и быстрее приближается к оси абсцисс при удалении от центра.
Часто вместо случайной величины Х целесообразно рассматривать нормированную случайную величину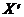 
, которую определяют как отношение отклонения к среднему квадратическому отклонению
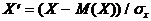. Нормированная величина имеет математическое ожидание, равное нулю и дисперсию, равную единице. При а=0 и
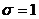нормальную кривую называют нормированной.
Ее уравнение:
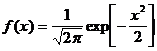
Между абсциссам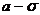и 
и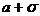 
расположено 68,27% всей площади кривой нормального распределения. Это означает, что 68,27% всех измеренных единиц отклоняется от среднего значения не более чем на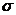, т.е. все они находятся в пределах 
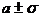. Площадь, заключенная между ординатами, проведенными на расстоянии 
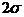с той и другой стороны от центра, составляет 0,9545, т.е. 95,45% всех единиц совокупности находятся в пределах 
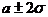. И наконец, 0,9973 или 99,73% всех единиц находятся в пределах 
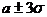. Это так называемое правило “трех сигм”, характерное для нормального распределения, согласно которому за пределами отклонения на 
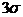находится не более 0,27% всех значений величин, иными словами, 27 реализаций на 10 тыс. испытаний. Исходя из принципа невозможности маловероятных событий такие события можно считать практически невозможными. На практике правило трех сигм применяют так: если распределение изучаемой случайной величины неизвестно, но условие, указанное в приведенном правиле, выполняется, то есть основание предполагать, что изучаемая величина распределена нормально; в противном случае она не распределена нормально.
