Поскольку параметры логнормального распределения в силу его асимметричности сложно использовать для статистических оценок, мы в дальнейшем будем использовать непрерывное начисление процента (с целью использования для работы нормального распределения!), поэтому волатильность - это выборочное стандартное отклонение логарифма отношения последней цены к цене предыдущей, выраженное в процентах годовых (стандартное отклонение непрерывной ставки процента):
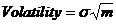[% годовых] Почему корень?
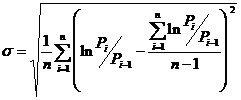, где
- m - количество периодов выбранного масштаба в рабочем году (260 для дневного масштаба, 52 - недельного, 12 - месячного, 6 240 - часового, 12 480 для тридцатиминутного и 187 200 для тикового);
- n - размер выборки (длина окна), принятой для расчета волатильности (10, 20, 40, 252 и т.д.).
Отдельно необходимо поставить вопрос о понятии выборки.
Из задачи “о блуждании случайной точки” известно, что среднее квадратическое отклонение длинного периода равно произведению среднего квадратического отклонения короткого периода на корень квадратный из числа блужданий. Тогда:
и, наконец,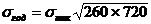
и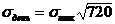 
,
если под тиком понимать совершение сделки каждые две минуты. Полагая, что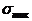
равно текущему среднему спрэду, можно определить 
,
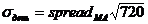или же по историческому среднему спрэду и исторической волатильности оценить количество совершенных за день сделок.
