Существование отношения Фибоначчи ФИ в геометрии очень хорошо известно. Однако подходящий для инвесторов способ применения этого отношения как геометрического инструмента к движению биржевых цен с использованием ФИ-спиралей и ФИ-эллип-сов до настоящего времени не публиковался. Чтобы применять ФИ-спирали и ФИ-эллипсы как аналитические инструменты, требуются квалификация программиста и сила компьютеров.
Поскольку компьютерные мощности сегодня легко доступны, препятствием является отсутствие не железа, а, скорее, некоторых знаний и соответствующего программного обеспечения.
Полностью готовый к работе пакет программ, прилагаемый к данной книге, позволяет каждому заинтересованному читателю/инвестору прослеживать приводимые примеры и генерировать подобные сигналы в торговле в режиме реального времени.
ФИ-спираль и ФИ-эллипс имеют необычные свойства, которые в соответствии с отношением Фибоначчи ФИ находятся в двух измерениях: цена и время. Весьма вероятно, что интегрирование ФИ-спирали и ФИ-эллипса намного повысит уровень интерпретации и использования отношения Фибоначчи. До сих пор отношение ФИ Фибоначчи в основном использовалось как инструмент для измерения коррекций и расширений ценовых колебаний. Прогнозы времени интегрировались редко, потому что они не представлялись столь же надежными, как анализ цен. Но с включением в геометрический анализ ФИ-спиралей и ФИ-эллипсов обе части — и ценовой, и временной анализ — могут комбинироваться правильно.
Чтобы лучше понять, как ФИ Фибоначчи геометрически встраивается в ФИ-спирали и ФИ-эллипсы, начнем с описания золотого сечения линии и прямоугольника и их соответствующих отношений к ФИ.
Греческий математик Евклид Мегарский (450—370 гг. до н. э.) — первый ученый, написавший о золотом сечении и, таким образом, сосредоточившийся на анализе прямой линии (рисунок 1.3).
Линия АВ длиной L разделена на два отрезка точкой С. Пусть длины АС и СВ будут равны а и b соответственно. Если С являет ся такой точкой, что частное L-т- а равно частному а -s-b, то С золотое сечение АВ. Отношение L -ь а или а -^ b называется золотым отношением.
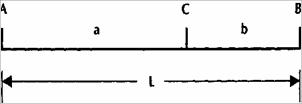
Рисунок 1.3 Золотое сечение линии. Источник: FAM Research, 2000.
Другими словами, точка С делит линию АВ на два отрезка таким образом, что отношения этих отрезков составляют 1,618 и 0,618; мы легко узнаем эти два числа по нашему анализу ряда суммирования Фибоначчи, как ФИ Фибоначчи и его обратное значение ФИ'.
Перемещаясь от одной колыбели науки к другой — из Древней Европы в Древнюю Африку или из Древней Греции в Древний Египет, мы узнаем, что в Великой Пирамиде Гизы прямоугольный этаж палаты фараона также иллюстрирует золотое сечение.
Золотое сечение прямоугольника лучше всего продемонстрировать, начертив квадрат, геометрическую конфигурацию, послужившую фундаментом Пирамиды Гизы. Этот квадрат можно затем преобразовать в золотой прямоугольник, как это схематично показано на рисунке 1.4.
