Эллиот и его последователи и не смогли договориться, должны ли исследования фигур графиков проводиться с использованием линейной и/или полулогарифмической шкалы.
Поскольку многие читатели не знакомы с этой проблемой, представляем два типичных недельных графика Индекса S&P500, чтобы продемонстрировать различие между линейной и полулогарифмической шкалами (рисунок 3.9).
На рисунке 3.9 один и тот же набор недельных данных Индекса S&P500 с июня 1996 года по декабрь 2000 года графически отражен дважды: с использованием линейной шкалы на верхнем графике и полулогарифмической на нижнем графике.
Шкалы на приведенном линейном графике показывают равные расстояния между всеми ценами от 700.00 до 1,500.00; на полулогарифмической шкале приращения уменьшаются по мере увеличения значений ценовой шкалы. Иными словами, на графике расстояние от 700.00 до 800.00 намного больше, чем расстояние от 1,400.00 до 1,500.00. Это означает: при работе с ценой и временем и измерении расстояния мы получаем на линейной и полулогарифмической шкалах разные результаты.
На первый взгляд, различия между двумя графиками не слишком большие. Но если измерить расстояние от впадины № 1 до пика №2 и определить эту длину как силу нашей импульсной волны, то на линейном графике впадина №3 достигает уровня восстановления 38,2%, а на полулогарифмическом — нет. То же явление можно увидеть в впадине №7: цена рынка не касается соответствующего уровня восстановления 38,2%.
Для ясности: коррекция цены на 38,2% импульсной волны в 1.000 тиков означает 382 тика, независимо от вида применяемого графического масштаба. Здесь представлен подход, при котором коррекции измеряются не в пунктах, а рассчитываются графически и геометрически измерением расстояний от максимумов до минимумов колебании в сантиметрах (или эквивалентных единицах).
Пример показывает, что длина импульсной волны от впадины №5 до пика №6 равна 3,9 см на линейной шкале и 3,4 см на полулогарифмической. Соответствующие коррекции 38,2% равны 1,5 см на линейной шкале и 1,3 см на полулогарифмической.
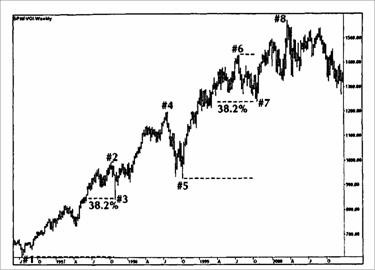
Рисунок 3.9 Линейное и полулогарифмическое отражение на примере недельного Индекса S&P500.
На линейной шкале корректирующее движение от пика № 6 к впадине № 7 равно 1,5 см, что делает его коррекцией, соответствующей уровню восстановления 38,2%. На полулогарифмической шкале, однако, корректирующий ход составляет только 1,1 см. Это означает, что уровень восстановления оказывается пропущен из-за узкого, но решающего разрыва в 0,2 см.
Такие искажения происходят на полулогарифмической шкале потому, что отправная точка полулогарифмической шкалы определяет конечное графическое отображение движения цены на графике.
Отправная точка полулогарифмической шкалы выбирается субъективно, независимо от того, хотим мы измерять расстояния в цене (вертикально) или во времени (горизонтально).
На линейных шкалах выбор отправной точки временного ряда не влияет на результат, потому что расстояние от одной до другой точки графика остается постоянным. С другой стороны, даже с учетом искажений, Эллиот сам указывал, что работа с полулогарифмическими шкалами может быть полезна, когда применяется в дополнение к линейному масштабу.
Теперь, когда все основные параметры коррекций как торговых инструментов подробно описаны, можно свести все вместе и проанализировать наборы данных разных продуктов различных сегментов международных рынков.
Анализ разделен на две секции: коррекции на дневной основе и коррекции на недельных данных.
