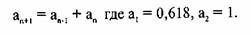Кратко напомним, как это подробно описано в Главе 1, что ряд суммирования Фибоначчи выглядит, как
1-1-2-3-5-8-13-21-34-55-89-144- . . .
На математическом языке это может быть написано, как
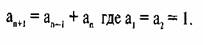
Ключевые свойства ряда суммирования Фибоначчи кратко можно сформулировать следующим образом:
• Каждое число, являющееся частью ряда суммирования Фибоначчи, при делении его на предшествующее значение (например, 13+8 или 21-ИЗ) дает отношение, которое мы округленно выражаем, как ФИ = 1,618 (зная, что осцилляция чисел последовательности Фибоначчи к отношению Фибоначчи ФИ асимптотический процесс).
• Отношение ФИ может быть выражено алгебраически формулой
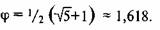
· Каждое число, являющееся частью ряда суммирования Фибоначчи, при делении его на последующее значение (например, 8:13 или 13 : 21) дает отношение, которое округленно выражаем, как ФИ' = 0,618 (то есть значение, обратное отношению ФИ).
• Отношение ФИ' может быть выражено алгебраически формулой
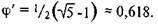
• Поскольку отношения ФИ и ФИ' являются обратными значениями, перемножение отношений ФИ и ФИ' дает единицу (ФИ х ФИ' = 1,618 х 0,618 = 1).
• Каждое число — часть ряда суммирования Фибоначчи (55— 34—21—13) — при делении его на значение, находящееся на два уровня ниже (например, 34+13 или 55 + 21), дает отношение, которое округленно выражаем, как 1 + ФИ = 2,618.
• Каждое число, являющееся частью ряда суммирования Фибоначчи (13—21—34—55), при делении его на значение, находящееся на два уровня выше (например, 13 - 34 или 21 - 55), дает отношение, которое округленно выражаем, как 1 — ФИ' = 0,382.
На основе двух последних свойств ряда суммирования Фибоначчи можно сгенерировать ряд ФИ, выглядящий следующим образом:
0,618-1,000-1,618-2,618-4,236-6,854-11,090-17,944-... На математическом языке это может быть выражено, как