Шестой инструмент — ФИ-эллипс — в своей геометрии подобен ФИ-спирали. Этот инструмент обсуждался в одном из более ранних разделов.
Эллипс — это математическое выражение овала. Когда мы имеем дело с инструментом Фибоначчи, нас главным образом интересует отношение ех=а-^-Ь большой оси эллипса а и его малой оси b (рисунок 1.20).
Эллипс превращается в ФИ-эллипс во всех тех случаях, когда отношение большой оси, деленной на малую ось эллипса, является элементным числом ряда ФИ — 0,618 — 1,000 — 1,618 — 2,618 и так далее. Круг в этом смысле особый тип ФИ-эллипса, в котором а = b (отношение а^-Ь = 1).
Эмпирические исследования показали, что большинство людей находят приближения ФИ-эллипсов значительно более удовлетворительными визуально. Это делает ФИ-эллипсы предпочтительнее всех других возможных эллипсов с отношениями большой оси, деленной на малую ось, иными, чем числа ряда ФИ. Но когда дело доходит до использования ФИ-эллипсов как инструментов рыночного анализа, в первую очередь мы ищем эллипсы, хорошо совпадающие с движениями рынка, которые можно использовать для прогнозирования.
По рисунку 1.20 можно заключить, что ФИ-эллипсы с увеличивающимися отношениями большой оси к малой оси ех = а-^Ь
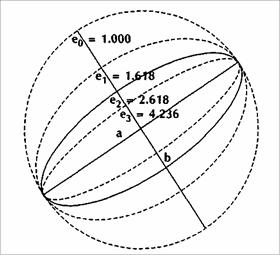
очень быстро превращаются в "гаванские сигары" и в этом процессе теряют часть своей привлекательности. ФИ-эллипсы, построенные на отношениях 6,854 и выше, становятся настолько узкими, что вряд ли могут применяться как аналитические инструменты графиков. На рисунке 1.21, однако, представлен убедительный подход, помогающий решить эту дилемму и позволяющий поддерживать привлекательность ФИ-эллипсов по крайней мере до отношений 17,944.
Чтобы заставить ФИ-эллипсы работать в качестве инструментов анализа графиков, преобразуем базовую математическую формулу, описывающую форму эллипса. Мы по-прежнему рассматриваем отношение большой оси эллипса а к его малой оси Ь, но иначе — через математическое выражение ех = (а-=-Ь)*.
мЮВЮКН

