Решая уравнение, получаем, что r= 11,5%. Аналогичным образом определяется теоретическая ставка спот для каждого следующего периода. Запишем использованное уравнение в общем виде:
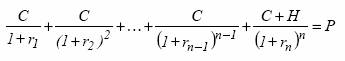
где С — купон облигации, до погашения которой осталось n
периодов;
Р — цена купонной облигации;
H — номинал купонной облигации;
r1 r2, ...,RN-1 — известные ставки спот для соответствующих периодов;
rn — ставка спот, величину которой требуется рассчитать.
Форвардная процентная ставка — это ставка для периода времени в будущем, которая определяется ставкой спот.
Пример. Ставка спот на один год составляет 10%, на два — 11%.
Определить форвардную ставку для второго года (то есть ставку
спот, которая будет на рынке через год для облигации с нулевым
купоном, выпущенной на год).
Допустим, вкладчик покупает облигацию с нулевым купоном,
выпущенную на два года, которая будет погашена по цене 1000 руб.
Тогда в начале двухлетнего периода он инвестирует сумму, равную
1000 : (1,11)2 = 811,62 руб.
Инвестор может выбрать иную стратегию, а именно, купить
облигацию сроком на один год и далее реинвестировать полученные от погашения облигации средства еще на один год. Ему безразлично, какую стратегию выбрать, если во втором случае он
также получит через два года 1000 руб., инвестировав сегодня
811,62 руб. Чтобы ответить на вопрос, под какой процент ему
следует реинвестировать средства на второй год, составим следующее уравнение:
1000 = 811,62 (1 + 0,1) (1 +re),
где re — форвардная ставка через год.
Решая уравнение, получаем re = 12%.
Запишем уравнение несколько иначе. Поскольку начальная
сумма инвестиций и итоговая сумма, которую вкладчик получит
через два года, равны, то должно выполняться равенство
