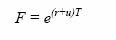Чтобы инвестор был безразличен к выбору первого или второго варианта, он
должен иметь одинаковый финансовый результат в конце периода
Т. Если отсутствует возможность совершить арбитражную операцию, то приведенная стоимость будущих позиций инвестора должна быть равна в начале периода 7, то есть
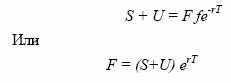
Приведем более строгое доказательство данных формул. Допустим, имеется два портфеля. Портфель А состоит из длинного
форвардного контракта на одну единицу серебра и суммы денег,
равной Ке-rT . Портфель Б состоит из одной единицы серебра S и
приведенной стоимости суммы, которую инвестор должен заплатить в конце периода Т за хранение и страховку товара. К концу
периода 7 портфель А будет состоять из одной единицы серебра,
поскольку сумма K используется для оплаты товара по контракту.
Портфель Б также состоит из одной единицы серебра. Поскольку
в конце периода стоимость портфелей равна, то она должна быть
равна и в начале периода Т, то есть
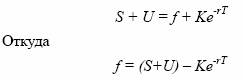
Поскольку в момент открытия позиции f= 0, а цена поставки
равна форвардной цене, то

Если складские расходы и страховка в любой момент времени
пропорциональны цене товара то формула (20) принимает вид
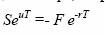
где и — расходы на хранение и страховку товара какие прерывно
начисляемый процент от его стоимости в расчете на год.
Тогда можно записать, что