Среднее значение случайной величины определяется по формуле
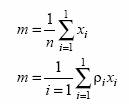
если одно и то же значение случайной величины встречается в
испытаниях несколько раз. В этом случае рi — удельный вес испытаний с результатом хi в общем числе испытаний.
Наиболее часто для расчета стандартного отклонения цены используют два приема. Первый состоит в том, что в качестве переменной величины принимают отношение изменения цены к ее
предыдущему значению, то есть
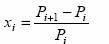
где Pi — цена актива в конце i-го периода.
Второй метод заключается в том, что в качестве переменной
принимают логарифм отношения последующей цены к предыдущей, а именно
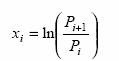
Расчеты, получаемые с использованием первого или второго
приема, не сильно отличаются друг от друга. Первый прием представляет собой не что иное, как начисление процента через определенные равные промежутки времени. Второй прием заключает в
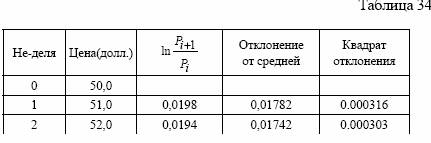
себе непрерывное начисление процента. Приведем пример расчета стандартного отклонения с использованием натурального логарифма. Схема расчета представлена в таблице 34. Значения цены
рассматриваются за десять недель.