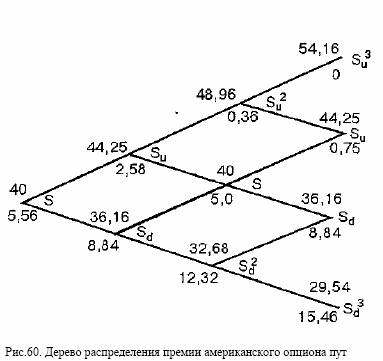
Для точки S (начало периода Δt3) расчетная цена равна 4,62

долл., однако в случае его исполнения в этот момент инвестор

получит прибыль, которая составит:

45 долл. - 40 долл. = 5 долл.

Следовательно, при таком развитии событий американский опцион будет стоить не 4,62 долл, а 5 долл. и его оптимально исполнить. Для точки Sd2 премия опциона должна быть не меньше чем:

45 долл. - 32,68 долл. = 12,32 долл.

Для точки Sd при немедленном исполнении опцион стоит:

45 долл. -36,1бдолл.= 8,84долл.

Его расчетная цена составляет:

(0,5163 × 5,0 + 0,4837 × 12,32) е-0,1 ×0,0833 =8,47 долл.

Следовательно, он должен стоить не меньше 8,84 долл.

В точке Su при немедленном исполнении опцион стоит:

45 долл. - 44,25 долл. = 0,75 долл.

Однако расчеты показывают, что в этом случае исполнение не

является оптимальной стратегией и цена опциона должна составить не 0,75 долл., а

(0,5163 × 0,36 + 0,4837 × 5,0) е-0,1 ×0,0833 = 2,58 долл

В итоге получаем — цена американского опциона пут в момент

заключения контракта равна 5,56 долл.

Мы рассмотрели биноминальную модель оценки премии опциона для акций, не выплачивающих дивиденды. В нашем примере

весь период опционного контракта, который насчитывал три месяца, был разбит на три периода. На практике для определения

цены опциона период Т необходимо разбить на большее число

периодов Δt. Обычно деление опционного контракта на 30-50

интервалов дает приемлемый результат.

 

 





[an error occurred while processing this directive] [an error occurred while processing this directive]