Концепция арбитража в математической теории эффективного рынка

О концепция арбитража в математической теории
эффективного рынка дна из важных черт современной финансовой теории состоит в применении математических методов. В результате многим экономическим понятиям и фактам удалось придать точный смысл, построить математические модели финансовых рынков, в том числе модель эффективного рынка. Помимо конкретных значимых результатов таких, например, как формула Блэка - Шоулза для оценки опционов, математическая формализация привела к созданию понятийной системы, в рамках которой возможно выдвижение и проверка количественных и качественных гипотез относительно финансового рынка. В методологическом плане эти достижения сблизили финансовую теорию с естественными науками.

Симптоматичным здесь выглядит появление такой новой научной дисциплины, как эконофизика, изучающая закономерности наблюдаемых финансовых явлений с интенсивным использованием математического аппарата (см. [1]*).
Практически все фундаментальные результаты теории эффективного рынка в той или иной мере опираются на понятие арбитража. Говоря неформально, отсутствие арбитражных возможностей означает, что извлечение прибыли без риска и без инвестирования капитала невозможно. Формализация понятия арбитража и установление критериев отсутствия арбитражных возможностей не только привели к уточнению самого этого понятия, но позволили также выявить существенные характеристики финансового рынка.

В частности, стала ясна ключевая роль гипотезы мартингальности, лежащей в основе большинства употребительных моделей современной финансовой математики (см. [2], [3]).
В данной заметке статье мы проследим, как происходит переход от неформального интуитивно ясного понимания арбитража к его мартингальной трактовке.
Одна из задач, с которыми столкнулась современная финансовая математика, – определение объективно обоснованных цен производных финансовых инструментов. A priori предполагается, что обоснованные цены могут быть установлены лишь тогда, когда рынок не допускает арбитражных возможностей. Рассмотрим платежное обязательство европейского типа C со роком исполнения T и платежной функцией f(ST), где ST–вектор цен основных рисковых активов в момент времени t=T.

Предположим, что из основных активов можно сформировать портфель , стоимость которого в текущий момент времени t=0 составляет V0(), и, не инвестируя дополнительных средств, управлять этим портфелем так, что в момент времени t=T его стоимость VT() окажется больше, чем f(ST). Тогда (в отсутствие арбитражных возможностей) должно выполняться соотношение
V0(C)V0(),
где V0(C)–стоимость платежного обязательства C в момент времени t=0. Если обозначить через Cверх. нижнюю границу стоимости таких портфелей в момент времени t=0, то мы придем к соотношению
V0(C)Cверх..
Величину Cверх. называют верхней ценой платежного обязательства C. Аналогично определяется нижняя цена Cниж.. Если контракт на поставку платежного обязательства C продан по цене, превышающей Cверх., продавец контракта может получить арбитражный доход (в англоязычной литературе – free lunch). Если контракт продан по цене ниже Cниж., арбитражный доход может получить покупатель.

Цены в промежутке от Cниж. до Cверх. приемлемы как для продавца, так и для покупателя контракта.
Таким образом, выполнение неравенств Cниж.Cверх. для всех платежных обязательств C означает, что на рынке могут быть установлены цены, не допускающие арбитража. По существу, это условие тавтологично (и даже тривиально). Тем более удивительным представляется тот факт, что оно открывает путь к первой фундаментальной теореме теории расчетов финансовых активов (APT - Arbitrage Pricing Theory).

По существу, если не вдаваться в технические детали, эта теорема утверждает, что финансовый рынок не допускает арбитража в том и только в том случае, когда в пространстве событий, происходящих на рынке, можно ввести вероятностную меру, относительно которой процесс изменения дисконтированных цен основных активов является мартингалом, и при этом вероятность невозможных событий равна нулю, а вероятность достоверных событий равна единице (такие меры называют мартингальными). Оказывается, существование мартингальной меры равносильно наличию в некотором смысле рационального прогноза цен.
Здесь мы сталкиваемся с одной довольно распространенной в математике трансформацией: факт, первоначально установленный как характеристическое свойство некоторого класса объектов, превращается в обобщающее определение, улавливающее глубинные свойства определяемого понятия. Если проанализировать текущую литературу, подобный процесс происходит с конепцией мартингальности.
Для дальнейшего изложения нам потребуются некоторые понятия современной финансовой математики. Базисом большинства моделей финансового рынка, функционирующего в условиях неопределенности, служит поток информации (It)t0 , в котором It–алгебра событий, известных к моменту времени t. Информационные алгебры It являются подалгебрами пространства возможных событий I, составленных из элементарных событий некоторого универсального пространства . В стохастических моделях на пространстве событий считается заданной вероятность P, относительно которой (,I,P)–вероятностное пространство.
Общепринятым стало использование так называемых (B,S)-моделей (или (B,S)-рынков). Основными инструментами на (B,S)-рынке являются безрисковый актив B=(Bt) и набор рисковых активов

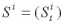
, i=1,2,…,k. Полагая B0=1, приведенное значение цены рискового актива можно записать в виде

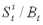
. Чтобы избежать излишних технических сложностей, мы будем рассматривать (B,S)-рынок с дискретным временем, на котором все события происходят в моменты времени t=0,1,…,T. Разница между безрисковым активом и рисковыми активами проявляется в том, что значение Bt предсказуемо, то есть полностью определяется информацией It–1, в то время как

можно определить, лишь владея всей информацией It. Дисконтированные цены St/Bt образуют мартингал, если математическое ожидание величины St/Bt в момент времени t–1 равно St–1/Bt–1.
Понятие мартингала допускает прозрачную содержательную интерпретацию в терминах прогноза. Предположим, что с использованием доступной информации формируются прогнозные значения различных величин, связанных с функционированием рынка. Обозначим через Progt(X) прогноз значения величины X в момент времени t, сделанный на основе информации It.

Укажем некоторые естественные свойства прогноза. Приведенные далее три свойства прогноза представляются достаточно очевидными.
Прогноз, сделанный в момент времени t=, когда значение X величины X уже известно, должен совпадать с этим значением:
Prog(X)=X.
Если прогнозируемая величина X не зависит от текущей информацииIt, t=0,1,…,–1, прогноз, сделанный в начальный момент времени, должен сохраняться для всех моментов времени, предшествующих :
Progt(X)=Prog0(X).
Прогноз должен обладать свойством линейности в том смысле, что прогноз линейной комбинации нескольких величин должен совпадать с соответствующей линейной комбинацией прогнозов:
Progt(aX+bY)=aProgt(X)+bProgt(Y).
Следующее свойство, выражающее согласованность прогнозов, является клчевым для понимания мартингальности.
Прогноз Progt(X) можно рассматривать как некоторую специфическую величину, связанную с рынком, и прогнозировать ее. В момент времени t прогноз Progt(X) должен совпадать с прогнозом следующего прогноза:
Progt(X)=Progt(Progt+1(X)) при t.

Если предположить, что в пространстве событий имеется вероятностная мера P*, относительно которой прогноз Progt(X) является математическим ожиданием величины X в момент времени t, то P* оказывается мартингальной мерой. Обратно, если имеется мартингальная вероятностная мера P*, то условное математическое ожидание E*(X|It) относительно этой меры обладает свойствами прогноза.
Таким образом, безарбитражность рынка оказывается в определенном смысле эквивалентной наличию рационального прогноза.
Основы современной математической теории финансов были заложены Л.Башелье в его работах, написанных в начале двадцатого ХХвека. Л. Башелье предполагал, что цены рисковых активов совершают броуновское движение. Цена производных инструментов в модели Башелье вычисляется как математическое ожидание.

Базовая эвристическая вероятностная мера на пространстве событий в модели Башелье мартингальна, поэтому вычисляемые так цены оказываются безарбитражными. Расхождение движения цен активов в модели Башелье и на реальных рынках привели к уточнению модели.
В основу нового поколения моделей диффузионного типа легли работы Ф.Блэка, Р. Мертона, М. Шоулза, выполненные в 70-х годах прошлого прошедшего века (и отмеченные в 1997 году. Нобелевской премией по экономике). Модель Блэка-Мертона-Шоулза строится на предположении о том, что процесс изменения цен рисковых активов является винеровским.

Техника стохастических дифференциальных уравнений и принцип безарбитражности позволяют свести задачу оценки производных инструментов к нахождению решения уравнения диффузии. В моделях диффузионного типа эвристическая вероятность, вообще говоря, не является мартингальной. Поэтому естественные цены производных инструментов, рассчитанные как соответствующие математические ожидания, допускают арбитраж.

Тем не менее, на пространстве событий может быть введена мартингальная мера, которая и приводит к справедливым ценам.
Подобный подход, использованный Коксом, Россом и Рубинштейном в биномиальной модели, поначалу казался лишь удобным техническим приемом. Дальнейшее развитие стохастической финансовой математики показало, что идея мартингальности позволяет взглянуть на многие проблемы математической теории финансов с новых позиций (см [см.2]).
Так, перестал быть фатальным отказ от нормальности. Дело в том, что в основе упомянутых выше классических моделей лежат предположения о нормальности распределений тех или иных величин, связанных с рисковыми активами. Такого рода предположения не всегда и не вполне адекватны имеющемуся фактическому материалу. Например, отклонение от нормальности проявляется у эмпирических распределений в наличии тяжелых хвостов;.

Тяжелые хвосты возникают они при отказе от нормальности в нелинейных моделях типа ARCH, GARCH и подобных им (см. [4]). Интенсивно разрабатывается проблематика, связанная с использованием для финансового моделирования устойчивых распределений (распределений Леви – Парето), см.[5].
Впрочем, критике подвергается и сама идея стохастичности финансовых временных рядов, которым присущи фрактальность (см. [6]) и хаотичность в точном смысле нелинейных динамических систем (см. [7], [8]). С учетом этого математические модели финансовых рынков перестают быть чисто вероятностными и все более значимой становится концепция безарбитражности как наличия рационального прогноза, не апеллирующего непосредственно к вероятности. Такая трактовка открывает новые, достаточно неожиданные подходы к анализу финансовых рынков.

Например, наличие рационального прогноза может быть оценено численно (экспертным путем или a posteriori по совпадению прогноза с реальными данными). Тем самым, количественную оценку получает и отсутствие арбитражных возможностей.
ЛИТЕРАТУРА

Mantegna R.N., Stanley H.E. An Introduction to Econophysics. Correlations and
Complexity in Finance. Cambridge University Press, 2000, 148 pp.
Ширяев А.Н. Основы стохастической финансовой математики. Т. 1, 2.
М., 1998., тт. 1, 2, 1018 с.
Karatzas I., Shreve S.E. Methods of Mathematical Finance. Springer, 1998,. 415pp.
Gourieux C. ARCH Models and Financial Applications. Springer, 1997., 228pp.
Schoutens W. Levy Processes in Finance: Pricing Financial Derivatives.
Wiley, 2003., 196 pp.
Mandelbrot B.B. Fractals and Scaling in Finance. Springer, 1997, 551 pp.
Петерс Э. Хаос и порядок на рынках капитала:. Новый аналитический взгляд
на циклы, цены и изменчивость рынка: Пер. с англ. М.: Мир, 2000., 334 с.
Сорнете Д. Как предсказывать крахи финансовых рынков:. Критические события
в комплексных финансовых системах: Пер. с англ. М.: Интернет-Трейдинг, 2003, 400 с.

••

* Здесь и далее цифра указывает на источник или примечание в конце материала.

Содержание раздела