Эволюционный компонент биополя
Они похожи на вышеупомянутые замкнутые петли, сделанные из спирально закрученных веревок. Таким образом, линии поля обладают той же самой структурой, что и нити тороидальных узлов6. Тороидальные узлы можно визуализировать как нить, намотанную на поверхность тора.
Самый простой тороидальный узел показан на рисунке 3 (см. следующую страницу).
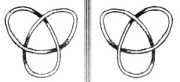
Все тороидальные узлы киральны, то есть, имеют левосторонний и право-сторонний вариант. Киральные струк-туры это такие структуры, у кото-рых отсутствует центр инверсии, это означает, что их зеркальное отраже-ние не идентично оригиналу. Таким образом, все киральные структуры яв-ляются двусимметричными формами, например, левая рука и правая рука (греческое слово kiros = рука), левосторонний и правосторонний шуруп, левосторонний и правосторонний узел (рисунки 3а и 3б), и так далее. Легко показать, что все математические решения уравнения (1) должны быть киральными: Дифференциальный оператор rot (= ротору) преобразовывает полярный вектор в аксиальный (осевой) (или наоборот), таким образом, k - это, фактически, не обычная скалярная константа это псевдоскаляр7. Каждый псевдоскаляр обладает киральными свойствами.
Когда константа k используется с противоположным знаком, мы получаем полностью эквивалентные решения, хотя и не идентичные они являются зеркальным отражением оригинала.
Можно показать, что для тороидальных решений, вышеописанная область интеграла сходится. Тороидальные решения хорошие решения для уравнения (1), ибо представляют собой нефиктивные полевые паутины, паутины с конечной энергией и нечувствительные к отдаленным пограничным условиям.
Здесь наблюдались только самые простые хорошие решения (тороидальные узлы), ибо они могут быть установлены умеренно простыми математическими инструментами. Также, для уравнения (1) могут существовать более сложные решения, например, заузленные структуры, не тороидальные и намного более сложные. Мы будем называть все эти заузленные структуры полевыми паутинами.
Легко видеть, что информационные паутины не излучают энергию. Вектор Направления8 выражается произведением векторов электрического и магнитного полей, но внутри информационной паутины, согласно уравнению (2), эти два поля полностью коллинеарны, и произведение их векторов обращается в нуль. Таким образом, в и вне этой паутины излучения не существует.
В этом случае паутина временно устойчива.
Являются ли такие структуры устойчивыми к внешним возмущениям? Могут ли такие возмущения медленно искажать и разрушать наши паутины? Ответ на эти вопросы не прямой. Давайте оговорим две подсказки:
(1) Информационные паутины связаны с эволюционными паутинами (подробнее об этом позже). Синтропические процессы в эволюционных паутинах обеспечивают их устойчивость, и, в результате, также стабилизируют информационные паутины.
(2) Мы изучили уравнения Максвелла в классическом пределе, но в действительности, магнитный поток в паутинах квантованный. Если петли заузленной структуры очень крошечные и если плотность магнитного потока маленькая, то через каждую петлю проходит только очень ограниченное количество магнитного квантового потока (флюксонов). Паутина может излучать только тогда, когда значительное возмущение изменило бы поток, по крайней мере, на один флюксон.
Фактически, оба объяснения в основном означают одно и то же. Синтропическая природа материи основа всех квантовых явлений. Сегодня мы все еще не можем говорить о детально разработанной теории квантовых процессов, интерпретированных посредством синтропической активности на субквантовом уровне (в субквантовом вакууме или, по другой терминологии, в эфире).
Но некоторые, уже появившиеся предварительные концепции многообещающи. Такая интерпретация намного ближе к некоторым альтернативным интерпретациям квантовой физики (например, в современные времена к школе Бома), чем к уже существующей “классической” копенгагенской интерпретации.
Мы видели, что уравнение (1) приводит к крайне интересным решениям и ситуациям. Как иллюстрацию, позвольте упомянуть о другом интересном приложении того же самого уравнения. Если мы монтируем тороидальную катушку, следуя линиям, являющимся решениями уравнения (1), то электрический ток в такой катушке полностью коллинеарен вектору магнитного поля, генерируемого этой же катушкой.
Такая катушка свободна от сил Лоренца, то есть, механически очень устойчива. Катушки такого типа иногда используются для генерирования очень сильных магнитных полей, если бы ограничивающим фактором9 могла быть механическая сила самой катушки.
В: ЭВОЛЮЦИОННЫЙ КОМПОНЕНТ БИОПОЛЯ
Здесь, ЭМ поле обладает структурой, похожей на информационные паутины (киральные узлы по крайней мере, частично тороидальные узлы). При некоторых условиях, эволюционная паутина может перерастать информационную. Основное условие для этого наличие в области паутины электрического заряда. До настоящего момента, мы обсуждали ЭМ поле в пустоте.
Изотропная однородная субстанция не могла бы изменить наши уравнения (потребовалось бы только прибавить диэлектрическую константу с). Это было бы даже более реальным, ибо биополе редко обнаруживается отделенным от биологической материи. Однако, наличие электрического заряда высокой подвижности вносит критическую новизну в наши уравнения: этот заряд рассеивается преимущественно только в ЭМ поле паутинообразной структуры.
Если в паутине соблюдаются условия для синтропических процессов (см. ниже), в биополе начинается синтропическая самоорганизация. Это нечто большее, чем просто обычная самоорганизация протеиновых структур (autopoiesis10) или самоорганизация в рассеивающихся структурах11 Пригожина. Все три установленных явления (autopoiesis, самоорганизация Пригожина и синтропическая самоорганизация) происходят, когда материя далека от термодинамического равновесия. Это очевидно для всех трех процессов самоорганизации.
Разница в том, что синтропические процессы (в отличии от двух других) сами создают состояние, далекое от термодинамического равновесия12. Первичное нарушение равновесия может вноситься колебанием, превышающим определенный порог. С этого момента, нарушение равновесия продолжается без какого-либо внешнего вмешательства.
Синтропические процессы, создающие новые эволюционные паутинообразные структуры, происходят при следующих условиях:
наличие электрического заряда высокой подвижности
низкая масса несущих заряд частиц
киральная симметрия с паутинообразной структурой
ориентированный во времени паттерн ЭМ вибрации (стрела времени в
паутинообразной структуре)
квантовая связанность в состояниях заряженных частиц (длина
связанности превышает период заузленной структуры)
адекватная амплитуда плотности магнитного поля.
Третье условие выполняется с самого начала, ибо структура информационного компонента уже киральная. И все же, четвертое условие (стрела времени) выполняется не автоматически. Однако, адекватное первичное колебание создает стрелу времени, и с этого момента, становятся возможными все последующие синтропические процессы самоорганизации. Немного позже мы будем описывать это колебание более детально.
Наше описание будет основываться на современной теории хаоса.
Третье и четвертое условия представляют собой требуемые свойства пространственно-временной симметрии паутинообразной структуры. Они предписываются некоторыми основными физическими законами (неизменность единичных преобразований пространства и времени). В совершенном квантовом состоянии заряженной частицы должны быть отражены паттерны структуры с требуемой симметрией пространства-времени, но это возможно только тогда, когда длина связанности квантового состояния превышает, по крайней мере, размер отдельных узлов, а связанность времени по крайней мере, один период ЭМ колебания.
Этот факт приводит к пятому условию. Несомненно, квантовая связанность чисто квантовый эффект и не обладает никакой классической аналогией13. Причина этому - особая информационная взаимосвязь в квантовых состояних; такая взаимосвязь не имеет места в классическом мире.
Квантовая связанность вносит в физику совершенно новые понимания давайте вспомним Аспекта и другие экперименты14, относящиеся к Восприятию Удаленных Электрических волн.
Второе и шестое условия взаимосвязаны: Необходимая амплитуда магнитного поля обладает некоей связанностью с массой заряженных частиц и с размером петель заузленной структуры. Чем больше масса и меньше размер петель, тем больше результирующее критическое поле (больше о критическом поле позже). Все это работало бы только с электронами, если бы петли были очень большими, но, как следствие, длина связанности тоже должна была быть большой. Такого рода эффект мог быть возможен в сверхпроводящих материалах. Температурное группирование сверхпроводящих пар Купера и атомов материи незначительно; следовательно, в этом случае происходила бы только самоорганизация электронного газа (без группирования с сетью).
Несмотря на это, такой гипотетический процесс в сверхпроводниках предлагает невероятные возможности для обработки информации. Совсем не глупо предположить, что нечто похожее происходит в меланиновых белковых структурах нервной ткани (Коуп).
- Вариант процессов самоорганизации
- Оба компонента биополя связаны
- Структуры непрерывно изменяют свою форму
- Примеры синтропического поведения
- Элегантное обретение силы. Эволюция сознания
