Классическим примером простейшей задачи системного анализа в условиях определенности может служить задача производства и поставок товара. Пусть некоторая фирма должна производить и поставлять продукцию клиентам равномерными партиями в количестве N =24000 единиц в год. Срыв поставок недопустим, так как штраф за это можно считать бесконечно большим.
Запускать в производство приходится сразу всю партию, таковы условия технологии. Стоимость хранения единицы продукции Cx=10 копеек в месяц, а стоимость запуска одной партии в производство (независимо от ее объема) составляет Cp =400 гривен.
Таким образом, запускать в год много партий явно невыгодно, но невыгодно и выпустить всего 2 партии в год — слишком велики затраты на хранение! Где же “золотая середина”, сколько партий в год лучше всего выпускать?
Будем строить модель такой системы. Обозначим через n размер партии и найдем количество партий за год —
p = N / n = 24000 / n.
Получается, что интервал времени между партиями составляет
t = 12 / p (месяцев), а средний запас изделий на складе — n/2 штук.
Сколько же нам будет стоить выпуск партии в n штук за один раз?
Сосчитать нетрудно — 0.1 · 12 · n / 2 гривен на складские расходы в год и 400p гривен за запуск партий по n штук изделий в каждой.
В общем виде годовые затраты составляют
E =
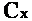
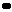 T
T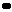 n / 2 +
n / 2 + 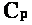
 N / n {3 - 2}
N / n {3 - 2}где T = 12 — полное время наблюдения в месяцах.
Перед нами типичная вариационная задача: найти такое n0, при котором сумма E достигает минимума.
Решение этой задачи найти совсем просто — надо взять производную по n и приравнять эту производную нулю. Это дает
n0 =
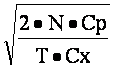 , {3 - 3}
, {3 - 3}что для нашего примера составляет 4000 единиц в одной партии и соответствует интервалу выпуска партий величиной в 2 месяца.
