Столь же легко понять необходимость условия m < k, объяснимого на простом примере аналогии — если мы исследуем некоторые предметы с использованием всех 5 человеческих чувств, то наивно надеяться на обнаружение более пяти “новых”, легко объяснимых, но неизмеряемых признаков у таких предметов, даже если мы “испытаем” очень большое их количество.
Вернемся к исходной матрице наблюдений E[n·k] и отметим, что перед нами, по сути дела, совокупности по n наблюдений над каждой из k случайными величинами E1, E2, … E k. Именно эти величины “подозреваются” в связях друг с другом — или во взаимной коррелированности.
Из рассмотренного ранее метода оценок таких связей следует, что мерой разброса случайной величины E i служит ее дисперсия, определяемая суммой квадратов всех зарегистрированных значений этой величины S(Eij)2 и ее средним значением (суммирование ведется по столбцу).
Если мы применим замену переменных в исходной матрице наблюдений, т.е. вместо Ei j будем использовать случайные величины
Xij =
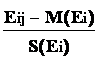, {3-27}то мы преобразуем исходную матрицу в новую
X[n·k] {3-28}
X 11
X12
…
X1i
…
X1k
X 21
X22
…
X2i
…
X2k
…
…
…
…
…
…
X j1
Xj2
…
Xji
…
Xjk
…
…
…
…
…
…
X n1
Xn2
…
Xni
…
Xnk
Отметим, что все элементы новой матрицы X[n·k] окажутся безразмерными, нормированными величинами и, если некоторое значение Xij составит, к примеру, +2, то это будет означать только одно - в строке j наблюдается отклонение от среднего по столбцу i на два среднеквадратичных отклонения (в большую сторону).
