Пусть конкурент назначил за первый объект очередную сумму X. Если мы не добавим небольшую сумму (минимальную надбавку D), то первый объект достанется конкуренту. При этом у конкурента в запасе останется сумма SB - X. Доход конкурента составит при этом (без учета D) DB = С1 - X.
Мы наверняка купим второй объект, если у нас в кармане
SA = (SB - X) + D, то есть немного больше, чем осталось у конкурента.
Значит, мы будем иметь доход DA = C2 - (SB - X) и разность доходов в этом случае составит
DA - DB = C2 - C1 - SB + 2·X . {3-20}
Ясно, что эта разность будет положительна только тогда, когда мы уступим первый объект за цену
X >
, {3-21}но никак не меньше.
· Будем повышать цену за первый объект до суммы X+ D с целью купить его.
Наш доход составит при этом
DA = C1 - (X + D).
Второй объект достанется конкуренту за сумму
SA - (X + D) + D,
так как ему придется поднять цену за этот объект до уровня, чуть большего остатка денег у нас.
Доход конкурента составит
DB = C2 - (SA - (X + D) + D),
а разность доходов составит (без учета D)
DA - DB = (C1 - X) - (C2 - SA + X) = С1 - С2 + SA - 2X . {3-22}
Эта разность будет положительна при условии
X <
, {3-23}Мы нашли две "контрольные" суммы для того, чтобы знать — когда надо пользоваться одной из двух доступных нам стратегий — выражения {3-21} и {3-23}. Среднее этих величин составит
K =
+ 
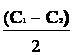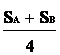{3-24}и определяет разумную границу для смены стратегий нашего участия в аукционе с целью одновременно получить доход себе побольше, а конкуренту — поменьше.
Интересно сосчитать свой доход и разность доходов на этой границе.
· Если мы уступили первый объект на этой границе, то по {3-20}
DA - DB = C2 - C1 - SB + 2K = 0.5(SA - SB).
· Если же мы купили первый объект на этой границе, то по {3-22}
DA - DB = С1 - С2 + SA - 2K = 0.5(SA - SB).
