И, наконец, Колонка 1 показывает сумму всех основных движений в каждом бычьем рынке. Очевидно, что такое число значительно больше, чем чистая разность между самым большим и самым маленьким значениями в любом бычьем рынке. Например, бычий рынок, рассмотренный в главе II, начался (для промышленности) с отметки 29.64 и закончился значением 76.04, и разница или чистое продвижение было равно 46.40 пункта. Сейчас это продвижение было разбито на четыре основных отрезка по 14.44, 17.33, 18.97 и 24.48 пункта соответственно.
Сумма этих отрезков равна 75.22, что и показано в колонке 1. Если 46.40 разделить на 75.22, то в результате получим 1.621, что и показано в процентах в колонке 1. Допустим,
что два инвестора были безошибочны в своих рыночных операциях, и что один купил акции на нижней отметке бычьего рынка и удерживал их до самой верхней отметки этого
рынка, перед тем, как продать. Обозначим его прибыль за 100%. Теперь допустим, что другой инвестор купил акции на самой низкой отметке и продавал их на вершине каждого
основного отрезка, и вновь покупал те же самые акции на нижней отметке каждой коррекции – его прибыль будет равна 162.1, в сравнении с 100, реализованных первым
инвестором. Таким образом, общая сумма коррекций откатывается на 62.1% от чистого роста. [Числа выделены авторами курса]
Итак, в 1936 году Роберт Ри открыл, не зная этого, пропорцию Фибоначчи и ее функцию относящую бычью фазу к медвежьей как по времени, так и по амплитуде. К счастью, он
чувствовал, что представленные данные обладают определенной ценностью, хотя и не имеют немедленной практической выгоды, но смогут быть полезными когда-нибудь в будущем. Так же и мы чувствуем, что есть многое, что следует познать в области пропорций, и наше введение, которое лишь зацепило верхний слой, может оказаться полезным некому будущему аналитику в ответах на вопросы, которые мы еще даже не поставили.
Пропорциональный анализ обнаружил несколько точных ценовых соотношений, которые часто происходят среди волн. В нем существует две категории соотношений: соотношение откатов и соотношение среди подволн.
Откаты
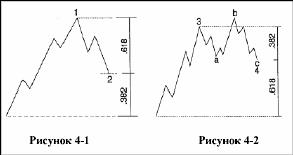
Подчас коррекции откатываются на величину некоторого процента Фибоначчи от предыдущей волны. Как показано на рис.4-1, резкая коррекция стремится откатиться на 61.8% или на 50% от предыдущей волны, особенно, когда происходит в качестве подволны 2 импульсной волны, в подволне В зигзага или в подволне Х в многократном зигзаге. Боковые коррекции чаще стремятся откатиться на 38.2% от предыдущей импульсной волны, особенно, когда они происходят в качестве волны 4, как показано на рис.4-2.
Коррекции бывают разных размеров. Пропорции, показанные на рис.4-1 и 4-2 являются только тенденциями, хотя именно им большинство аналитиков уделяют чрезмерное внимание из-за простого их вычисления. Тем не менее, гораздо более точными и достоверными являются соотношения между чередующимися волнами или длинами волн, раскрывающихся в одном направлении, как разъясняется в следующем разделе.
