Исключаем из матрицы
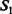
представлен на рис. 9.6, г. Повторяем описанные выше действия, что приводит к замене единицей единственного нуля.
Не приводя промежуточного рисунка, отметим, что мы подтвердили высоким (единичным) весом связи А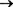1 
1, 1R1. 
2. Произведем трассировку [А1,
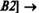
Сформируем матрицу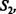 
Строка, соответствующая нейрону 1, содержит одну единицу, при том, что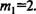 
Присваиваем строкам — входам матрицы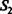 
= 2. Присваиваем нейрону 2 признак «возбужден», а нейроны А1 и В2 исключаем из рассмотрения. Среди оставшихся строк исключаем «пустую», соответствующую нейрону 3 и не обладающую признаком «возбужден». Исключаем и соответствующий столбец. Матрица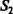 
Таким образом, в результате трассировки на данном шаге сложились связи с единичными весами А1 
2, 2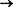 
3. Повторив алгоритм построений, легко найдем связи с единичными весами А2 
3, 3
4. Трассировка последнего пути возбуждения [А2, В2] 
в которой не отражены те нейроны, в строках которых число единиц меньше соответствующего значения т (рис. 9.6, з). Но ведь в ней вообще нет никаких связей!
Придется их ввести, да еще с единичными весами согласно условию задачи. Очевидно, что больше трех эталонов эта сеть воспринять не способна. Таким образом, мы вводим дополнительные связи с единичными весами А1 
R4.
