Шаг 7. Проверяем количество строк матрицы 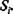
Шаг 8. Исключаем строки (и соответствующие им столбцы) матрицы 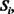
Шаг 9. Исключаем из матрицы 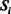
Шаг 10. Выделяем множество строк матрицы 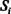
Шаг 11. В совокупности выделенных столбцов находим первую строку, содержащую максимальное число единиц и не содержащую единиц в других столбцах, т. е. число единиц в найденной строке и выделенных столбцах не должно быть меньше т. Соответствующий этой строке нейрон может быть использован повторно. Если таковой строки найти не удается, выполняем шаг 13.
Шаг 12. Исключаем из рассмотрения нейроны (вычеркиваем строки и столбцы), которым соответствуют единицы в найденной строке. Присваиваем нейрону, соответствующему выделенной строке, признак «возбужден». Уничтожаем в этой строке все нули и символы транзитивных связей, если они имеются. Строка преобразуется во вход матрицы 
Шаг 13. В совокупности выделенных столбцов находим первую строку, содержащую максимальное число нулевых элементов. Если такой строки нет, выполняем шаг 15.
Шаг 14. Меняем значения возбуждения соответствующих связей, т.е. заменяем нули единицами. Присваиваем нейрону, соответствующему выделенной строке, значение т, равное количеству единиц в строке, и признак «возбужден». Вычеркиванием строк и столбцов исключаем из рассмотрения нейроны, передавшие энергию возбуждения найденному. Примечание. Значения весов связей одного нейрона могут корректироваться лишь однажды. При обучении другим эталонам нейрон может использоваться повторно, если в обучении участвуют все нейроны, передающие ему возбуждение с весом, равным единице. При этом достаточно учитывать лишь число единиц в строке. В процессе такого обучения эталоны друг другу не мешают. Внесенные изменения весов учитываем в матрице S. Выполняем шаг 7.
Шаг 15. В каждом выделенном столбце находим первый сверху непустой элемент, соответствующий транзитивной связи. Вводим в нейросеть дополнительную связь, присваивая найденному элементу единичное значение. Исключаем из рассмотрения (вычеркиваем строки и столбцы) нейроны, соответствующие обработанным столбцам. Отражаем внесенные изменения в матрице S. Примечание. Указанная транзитивная связь (см. выше) потребуется на последней стадии обучения обобщенному эталону и может обнаружиться лишь в строке, соответствующей нейрону выходного слоя, поэтому формировать значение m уже излишне. Выполняем шаг 7.
Построенный алгоритм трассировки, несомненно, эвристический, т.е. дающий приблизительное, удовлетворительное решение. Точный алгоритм трассировки, минимизирующий число использованных нейронов и дополнительных связей, требует совместного анализа всех эталонов и решений, выделения и создания термов, участвующих в получении решений.
Так, в нашем примере удачно сложился терм в результате связи [C1, C2, С3, С4, С5 6]. Он использовался при получении трех — R1, R4, R5.
